روش نیوتن برای یافتن ریشه¶
این یک روش تکراری است که توسط اسحاق نیوتن در حدود سال ۱۶۶۴ ابداع شد. با این حال، این روش گاهی اوقات روش رافسون نیز نامیده میشود، زیرا رافسون همین الگوریتم را چند سال پس از نیوتن ابداع کرد، اما مقالهاش بسیار زودتر منتشر شد.
مسئله به شرح زیر است. با توجه به معادله زیر:
میخواهیم این معادله را حل کنیم. بهطور دقیقتر، میخواهیم یکی از ریشههای آن را بیابیم (فرض بر این است که ریشه وجود دارد). فرض میشود که $f(x)$ در بازه $[a, b]$ پیوسته و مشتقپذیر باشد.
الگوریتم¶
پارامترهای ورودی الگوریتم نه تنها شامل تابع $f(x)$ است، بلکه یک تقریب اولیه - مقداری $x_0$ - را نیز در بر میگیرد که الگوریتم با آن شروع میشود.
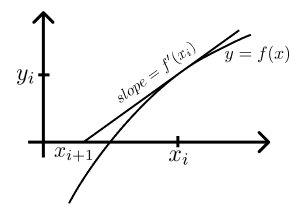
فرض کنید $x_i$ را محاسبه کردهایم، $x_{i+1}$ را به صورت زیر محاسبه میکنیم. خط مماس بر نمودار تابع $f(x)$ را در نقطه $x = x_i$ رسم کرده و نقطه تقاطع این مماس با محور $x$ها را پیدا میکنیم. $x_{i+1}$ برابر با مختصات $x$ نقطه یافتشده قرار داده میشود و ما کل فرآیند را از ابتدا تکرار میکنیم.
به دست آوردن فرمول زیر دشوار نیست،
ابتدا شیب $f'(x)$، یعنی مشتق $f(x)$ را محاسبه میکنیم و سپس معادله خط مماس را که به صورت زیر است، تعیین میکنیم،
مماس، محور xها را در مختصات $y = 0$ و $x = x_{i+1}$ قطع میکند،
حال، با حل این معادله مقدار $x_{i+1}$ را به دست میآوریم.
بهطور شهودی واضح است که اگر تابع $f(x)$ «خوب» (هموار) باشد و $x_i$ به اندازه کافی به ریشه نزدیک باشد، آنگاه $x_{i+1}$ حتی به ریشه مورد نظر نزدیکتر خواهد بود.
نرخ همگرایی از مرتبه دو است که به زبان ساده، به این معنی است که تعداد ارقام صحیح در مقدار تقریبی $x_i$ با هر تکرار دو برابر میشود.
کاربرد در محاسبه ریشه دوم¶
بیایید از محاسبه ریشه دوم به عنوان مثالی از روش نیوتن استفاده کنیم.
اگر $f(x) = x^2 - n$ را جایگزین کنیم، آنگاه پس از سادهسازی عبارت، به نتیجه زیر میرسیم:
اولین حالت متداول این مسئله زمانی است که یک عدد گویای $n$ داده شده و باید ریشه آن با دقت مشخص eps محاسبه شود:
double sqrt_newton(double n) {
const double eps = 1E-15;
double x = 1;
for (;;) {
double nx = (x + n / x) / 2;
if (abs(x - nx) < eps)
break;
x = nx;
}
return x;
}
حالت متداول دیگر مسئله زمانی است که نیاز به محاسبه ریشه صحیح داریم (برای $n$ دادهشده، بزرگترین $x$ را بیابید به طوری که $x^2 \le n$). در اینجا لازم است شرط توقف الگوریتم را کمی تغییر دهیم، زیرا ممکن است $x$ در نزدیکی پاسخ شروع به «پرش» کند. بنابراین، شرطی را اضافه میکنیم که اگر مقدار $x$ در مرحله قبل کاهش یافته و در مرحله فعلی سعی در افزایش دارد، الگوریتم باید متوقف شود.
int isqrt_newton(int n) {
int x = 1;
bool decreased = false;
for (;;) {
int nx = (x + n / x) >> 1;
if (x == nx || nx > x && decreased)
break;
decreased = nx < x;
x = nx;
}
return x;
}
در نهایت، به حالت سوم میرسیم - برای محاسبات با اعداد بزرگ (bignum). از آنجایی که عدد $n$ میتواند به اندازه کافی بزرگ باشد، توجه به تقریب اولیه منطقی است. بدیهی است که هر چه تقریب اولیه به ریشه نزدیکتر باشد، نتیجه سریعتر به دست میآید. روشی ساده و مؤثر این است که تقریب اولیه را برابر با عدد $2^{\textrm{bits}/2}$ در نظر بگیریم، که در آن $\textrm{bits}$ تعداد بیتهای عدد $n$ است. در ادامه کد Java که این حالت را نشان میدهد آمده است:
public static BigInteger isqrtNewton(BigInteger n) {
BigInteger a = BigInteger.ONE.shiftLeft(n.bitLength() / 2);
boolean p_dec = false;
for (;;) {
BigInteger b = n.divide(a).add(a).shiftRight(1);
if (a.compareTo(b) == 0 || a.compareTo(b) < 0 && p_dec)
break;
p_dec = a.compareTo(b) > 0;
a = b;
}
return a;
}
به عنوان مثال، این کد برای $n = 10^{1000}$ در $60$ میلیثانیه اجرا میشود، و اگر انتخاب بهبودیافته تقریب اولیه را حذف کنیم (یعنی فقط با $1$ شروع کنیم)، آنگاه حدوداً در $120$ میلیثانیه اجرا خواهد شد.