درخت پوشای کمینه - الگوریتم پریم¶
یک گراف وزندار و بدون جهت $G$ با $n$ رأس و $m$ یال داده شده است. شما میخواهید یک درخت پوشا از این گراف پیدا کنید که تمام رئوس را به هم متصل کرده و کمترین وزن را داشته باشد (یعنی مجموع وزن یالها کمینه باشد). یک درخت پوشا مجموعهای از یالهاست به طوری که از هر رأس بتوان دقیقاً از طریق یک مسیر ساده به هر رأس دیگری رسید. به درخت پوشا با کمترین وزن، درخت پوشای کمینه گفته میشود.
در تصویر سمت چپ میتوانید یک گراف وزندار بدون جهت و در تصویر سمت راست، درخت پوشای کمینه متناظر با آن را مشاهده کنید.
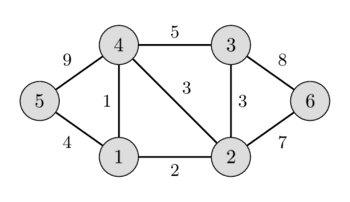
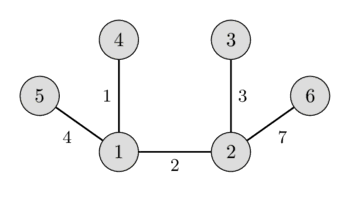
به راحتی میتوان دید که هر درخت پوشایی لزوماً $n-1$ یال خواهد داشت.
این مسئله به طور طبیعی در مسائل زیادی ظاهر میشود. برای مثال در مسئله زیر: $n$ شهر وجود دارد و برای هر جفت شهر، هزینه ساخت جاده بین آنها داده شده است (یا میدانیم که ساخت جاده بین آنها از نظر فیزیکی غیرممکن است). باید جادهها را طوری بسازیم که بتوان از هر شهر به هر شهر دیگری رفت و هزینه ساخت تمام جادهها کمینه باشد.
الگوریتم پریم¶
این الگوریتم در اصل توسط ریاضیدان چک، Vojtěch Jarník در سال ۱۹۳۰ کشف شد. با این حال، این الگوریتم بیشتر با نام الگوریتم پریم شناخته میشود که برگرفته از نام ریاضیدان آمریکایی، Robert Clay Prim است که آن را در سال ۱۹۵۷ دوباره کشف و منتشر کرد. علاوه بر این، Edsger Dijkstra نیز این الگوریتم را در سال ۱۹۵۹ منتشر کرد.
شرح الگوریتم¶
در اینجا الگوریتم را در سادهترین شکل خود توصیف میکنیم. درخت پوشای کمینه به تدریج و با افزودن یالها یکی پس از دیگری ساخته میشود. در ابتدا درخت پوشا تنها از یک رأس (که به صورت دلخواه انتخاب میشود) تشکیل شده است. سپس یالی با کمترین وزن که از این رأس خارج میشود، انتخاب شده و به درخت پوشا اضافه میشود. پس از آن، درخت پوشا شامل دو رأس خواهد بود. حالا یالی با کمترین وزن را انتخاب و اضافه میکنیم که یک سر آن در یک رأسِ از قبل انتخاب شده (یعنی رأسی که قبلاً جزئی از درخت پوشا شده) و سر دیگر آن در یک رأس انتخاب نشده قرار دارد. این روند به همین ترتیب ادامه مییابد، یعنی هر بار یالی با کمترین وزن را انتخاب و اضافه میکنیم که یک رأس انتخاب شده را به یک رأس انتخاب نشده متصل میکند. این فرآیند تا زمانی که درخت پوشا شامل تمام رئوس شود (یا معادل آن، تا زمانی که $n - 1$ یال داشته باشیم) تکرار میشود.
در پایان، درخت پوشای ساخته شده، کمینه خواهد بود. اگر گراف اصلی همبند نباشد، آنگاه درخت پوشایی وجود نخواهد داشت، بنابراین تعداد یالهای انتخاب شده کمتر از $n - 1$ خواهد بود.
اثبات¶
فرض کنید گراف $G$ همبند است، یعنی جواب وجود دارد. گراف حاصل از الگوریتم پریم را با $T$ و درخت پوشای کمینه را با $S$ نمایش میدهیم. واضح است که $T$ در واقع یک درخت پوشا و زیرگرافی از $G$ است. فقط باید نشان دهیم که وزنهای $S$ و $T$ یکسان هستند.
اولین باری را در الگوریتم در نظر بگیرید که یالی به $T$ اضافه میکنیم که جزئی از $S$ نیست. این یال را با $e$، دو سر آن را با $a$ و $b$ و مجموعه رئوس از قبل انتخاب شده را با $V$ نشان میدهیم ($a \in V$ و $b \notin V$ یا برعکس).
در درخت پوشای کمینه $S$، رئوس $a$ و $b$ با مسیری به نام $P$ به هم متصل هستند. در این مسیر میتوانیم یالی مانند $f$ پیدا کنیم که یک سر آن در $V$ و سر دیگرش خارج از $V$ باشد. از آنجایی که الگوریتم، $e$ را به جای $f$ انتخاب کرده است، به این معنی است که وزن $f$ بزرگتر یا مساوی وزن $e$ است.
یال $e$ را به درخت پوشای کمینه $S$ اضافه کرده و یال $f$ را حذف میکنیم. با افزودن $e$ یک دور ایجاد کردیم، و از آنجا که $f$ نیز بخشی از تنها دور موجود بود، با حذف آن، گراف حاصل دوباره بدون دور خواهد بود. و چون ما فقط یک یال از یک دور را حذف کردهایم، گراف حاصل همچنان همبند است.
درخت پوشای حاصل نمیتواند وزن کل بیشتری داشته باشد، زیرا وزن $e$ بیشتر از وزن $f$ نبود، و همچنین نمیتواند وزن کمتری داشته باشد زیرا $S$ یک درخت پوشای کمینه بود. این به این معنی است که با جایگزین کردن یال $f$ با $e$، ما یک درخت پوشای کمینه متفاوت تولید کردهایم. و وزن $e$ باید با وزن $f$ یکسان باشد.
بنابراین، تمام یالهایی که در الگوریتم پریم انتخاب میکنیم، وزنهای یکسانی با یالهای هر درخت پوشای کمینه دارند، که به این معنی است که الگوریتم پریم واقعاً یک درخت پوشای کمینه تولید میکند.
پیادهسازی¶
پیچیدگی الگوریتم به این بستگی دارد که چگونه یال کمینه بعدی را از میان یالهای مناسب جستجو میکنیم. رویکردهای متعددی وجود دارد که به پیچیدگیها و پیادهسازیهای متفاوتی منجر میشوند.
پیادهسازیهای ساده: $O(n m)$ و $O(n^2 + m \log n)$¶
اگر با پیمایش تمام یالهای ممکن به دنبال یال مورد نظر بگردیم، پیدا کردن یال با کمترین وزن $O(m)$ زمان میبرد. پیچیدگی کل $O(n m)$ خواهد بود. در بدترین حالت این برابر با $O(n^3)$ است که بسیار کند است.
این الگوریتم را میتوان بهبود بخشید اگر فقط به یک یال از هر رأس از قبل انتخاب شده نگاه کنیم. برای مثال، میتوانیم یالهای هر رأس را به ترتیب صعودی وزنشان مرتب کرده و یک اشارهگر به اولین یال معتبر (یعنی یالی که به یک رأس انتخاب نشده میرود) ذخیره کنیم. سپس پس از یافتن و انتخاب یال کمینه، اشارهگرها را بهروزرسانی میکنیم. این کار پیچیدگی $O(n^2 + m)$ و برای مرتبسازی یالها $O(m \log n)$ اضافه میکند که در بدترین حالت پیچیدگی $O(n^2 \log n)$ را به ما میدهد.
در ادامه دو الگوریتم کمی متفاوت را بررسی میکنیم، یکی برای گرافهای متراکم و دیگری برای گرافهای خلوت که هر دو پیچیدگی بهتری دارند.
گرافهای متراکم: $O(n^2)$¶
ما از زاویهای دیگر به این مسئله میپردازیم: برای هر رأس که هنوز انتخاب نشده است، یال با کمترین وزن به یک رأس از قبل انتخاب شده را ذخیره میکنیم.
سپس در هر مرحله، فقط باید به این یالهای با وزن کمینه نگاه کنیم که پیچیدگی آن $O(n)$ خواهد بود.
پس از افزودن یک یال، برخی از اشارهگرهای یال کمینه باید دوباره محاسبه شوند. توجه داشته باشید که وزنها فقط میتوانند کاهش یابند، یعنی یال با کمترین وزن برای هر رأس انتخاب نشده ممکن است همان باقی بماند یا با یک یال به رأس تازه انتخاب شده بهروز شود. بنابراین، این مرحله نیز میتواند در $O(n)$ انجام شود.
در نتیجه، به نسخهای از الگوریتم پریم با پیچیدگی $O(n^2)$ رسیدیم.
این پیادهسازی به ویژه برای مسئله درخت پوشای کمینه اقلیدسی (Euclidean Minimum Spanning Tree) بسیار مناسب است: $n$ نقطه روی یک صفحه داریم و فاصله بین هر جفت نقطه، فاصله اقلیدسی بین آنهاست و میخواهیم یک درخت پوشای کمینه برای این گراف کامل پیدا کنیم. این کار را میتوان با الگوریتم توصیف شده در زمان $O(n^2)$ و حافظه $O(n)$ حل کرد، که با الگوریتم کراسکال امکانپذیر نیست.
int n;
vector<vector<int>> adj; // ماتریس مجاورت گراف
const int INF = 1000000000; // وزن INF به معنی عدم وجود یال است
struct Edge {
int w = INF, to = -1;
};
void prim() {
int total_weight = 0;
vector<bool> selected(n, false);
vector<Edge> min_e(n);
min_e[0].w = 0;
for (int i=0; i<n; ++i) {
int v = -1;
for (int j = 0; j < n; ++j) {
if (!selected[j] && (v == -1 || min_e[j].w < min_e[v].w))
v = j;
}
if (min_e[v].w == INF) {
cout << "No MST!" << endl;
exit(0);
}
selected[v] = true;
total_weight += min_e[v].w;
if (min_e[v].to != -1)
cout << v << " " << min_e[v].to << endl;
for (int to = 0; to < n; ++to) {
if (adj[v][to] < min_e[to].w)
min_e[to] = {adj[v][to], v};
}
}
cout << total_weight << endl;
}
ماتریس مجاورت adj[][] با اندازه $n \times n$ وزن یالها را ذخیره میکند و اگر یالی بین دو رأس وجود نداشته باشد از وزن INF استفاده میکند.
الگوریتم از دو آرایه استفاده میکند: پرچم selected[] که نشان میدهد کدام رئوس را قبلاً انتخاب کردهایم، و آرایه min_e[] که برای هر رأس هنوز انتخاب نشده، یال با کمترین وزن به یک رأس انتخاب شده را ذخیره میکند (وزن و رأس مقصد را ذخیره میکند).
الگوریتم $n$ مرحله انجام میدهد، در هر تکرار، رأسی که کوچکترین وزن یال را دارد انتخاب شده و min_e[] برای تمام رئوس دیگر بهروزرسانی میشود.
گرافهای خلوت: $O(m \log n)$¶
در الگوریتم توصیف شده در بالا، میتوان عملیات یافتن کمینه و تغییر برخی مقادیر را به عنوان عملیات روی مجموعه (set) تفسیر کرد.
این دو عملیات کلاسیک توسط بسیاری از ساختمان دادهها پشتیبانی میشوند، برای مثال set در C++ (که از طریق درختهای قرمز-سیاه پیادهسازی شدهاند).
الگوریتم اصلی همان است، اما اکنون میتوانیم یال کمینه را در زمان $O(\log n)$ پیدا کنیم. از طرف دیگر، محاسبه مجدد اشارهگرها اکنون $O(n \log n)$ زمان میبرد که بدتر از الگوریتم قبلی است.
اما وقتی در نظر بگیریم که در کل فقط به $O(m)$ بهروزرسانی نیاز داریم و $O(n)$ جستجو برای یال کمینه انجام میدهیم، آنگاه پیچیدگی کل $O(m \log n)$ خواهد بود. برای گرافهای خلوت، این بهتر از الگوریتم بالا است، اما برای گرافهای متراکم کندتر خواهد بود.
const int INF = 1000000000;
struct Edge {
int w = INF, to = -1;
bool operator<(Edge const& other) const {
return make_pair(w, to) < make_pair(other.w, other.to);
}
};
int n;
vector<vector<Edge>> adj;
void prim() {
int total_weight = 0;
vector<Edge> min_e(n);
min_e[0].w = 0;
set<Edge> q;
q.insert({0, 0});
vector<bool> selected(n, false);
for (int i = 0; i < n; ++i) {
if (q.empty()) {
cout << "No MST!" << endl;
exit(0);
}
int v = q.begin()->to;
selected[v] = true;
total_weight += q.begin()->w;
q.erase(q.begin());
if (min_e[v].to != -1)
cout << v << " " << min_e[v].to << endl;
for (Edge e : adj[v]) {
if (!selected[e.to] && e.w < min_e[e.to].w) {
q.erase({min_e[e.to].w, e.to});
min_e[e.to] = {e.w, v};
q.insert({e.w, e.to});
}
}
}
cout << total_weight << endl;
}
در اینجا گراف از طریق یک لیست مجاورت adj[] نمایش داده میشود که در آن adj[v] شامل تمام یالها (به صورت زوجهای وزن و مقصد) برای رأس v است.
min_e[v] وزن کوچکترین یال از رأس v به یک رأس از قبل انتخاب شده را ذخیره میکند (دوباره به صورت زوج وزن و مقصد).
علاوه بر این، صف q با تمام رئوس هنوز انتخاب نشده به ترتیب افزایش وزن min_e پر میشود.
الگوریتم n مرحله انجام میدهد، در هر مرحله رأس v با کوچکترین وزن min_e را انتخاب میکند (با استخراج آن از ابتدای صف)، و سپس تمام یالهای این رأس را بررسی کرده و مقادیر را در min_e بهروزرسانی میکند (در حین بهروزرسانی، باید یال قدیمی را از صف q حذف کرده و یال جدید را وارد کنیم).