پرش به محتویات

اصل شمول و طرد

اصل شمول و طرد (Inclusion-Exclusion Principle) یک روش ترکیبیاتی مهم برای محاسبه اندازه یک مجموعه یا احتمال رویدادهای پیچیده است. این اصل، اندازه مجموعه‌های مجزا را به اندازه اجتماعشان مرتبط می‌سازد.

بیان اصل

فرمول کلامی

اصل شمول و طرد را می‌توان به صورت زیر بیان کرد:

برای محاسبه اندازه اجتماع چند مجموعه، لازم است اندازه این مجموعه‌ها را به‌طور جداگانه جمع کرده، سپس اندازه تمام اشتراک‌های دو به دو از مجموعه‌ها را کم کنیم، سپس اندازه اشتراک‌های سه‌تایی از مجموعه‌ها را اضافه کنیم، اندازه اشتراک‌های چهارتایی را کم کنیم و به همین ترتیب تا اشتراک تمام مجموعه‌ها ادامه دهیم.

فرمول‌بندی بر حسب مجموعه‌ها

تعریف بالا را می‌توان به صورت ریاضی به شکل زیر بیان کرد:

$$\left| \bigcup_{i=1}^n A_i \right| = \sum_{i=1}^n|A_i| - \sum_{1\leq i<j\leq n} |A_i \cap A_j| + \sum _{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k| - \cdots + (-1)^{n-1} | A_1 \cap \cdots \cap A_n |$$

و به شکلی فشرده‌تر:

$$\left|\bigcup_{i=1}^n A_i \right| = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}{\Biggl |}\bigcap_{j\in J}A_{j}{\Biggr |}$$

فرمول‌بندی با استفاده از نمودارهای ون

فرض کنید نمودار، سه مجموعه $A$، $B$ و $C$ را نشان می‌دهد:

نمودار ون

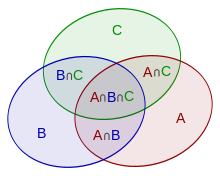
آنگاه مساحت اجتماع آنها $A \cup B \cup C$ برابر است با مجموع مساحت‌های $A$، $B$ و $C$ منهای مساحت‌هایی که دو بار پوشش داده شده‌اند یعنی $A \cap B$، $A \cap C$، $B \cap C$ و به علاوه مساحتی که سه بار پوشش داده شده است یعنی $A \cap B \cap C$:

$$S(A \cup B \cup C) = S(A) + S(B) + S(C) - S(A \cap B) - S(A \cap C) - S(B \cap C) + S(A \cap B \cap C)$$

این فرمول را می‌توان برای اجتماع $n$ مجموعه نیز تعمیم داد.

فرمول‌بندی بر حسب نظریه احتمال

اگر $A_i$ $(i = 1,2...n)$ پیشامدها باشند و ${\cal P}(A_i)$ احتمال وقوع پیشامد $A_i$ باشد، آنگاه احتمال اجتماع آنها (یعنی احتمال وقوع حداقل یکی از پیشامدها) برابر است با:

$$\begin{eqnarray} {\cal P} \left( \bigcup_{i=1}^n A_i \right) &=& \sum_{i=1}^n{\cal P}(A_i)\ - \sum_{1\leq i<j\leq n} {\cal P}(A_i \cap A_j)\ + \\ &+& \sum _{1\leq i<j<k\leq n}{\cal P}(A_i \cap A_j \cap A_k) - \cdots + (-1)^{n-1} {\cal P}( A_1 \cap \cdots \cap A_n ) \end{eqnarray}$$

و به شکلی فشرده‌تر:

$${\cal P} \left(\bigcup_{i=1}^n A_i \right) = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}\ {\cal P}{\Biggl (}\bigcap_{j\in J}A_{j}{\Biggr )}$$

اثبات

برای اثبات، راحت‌تر است که از فرمول‌بندی ریاضی بر حسب نظریه مجموعه‌ها استفاده کنیم:

$$\left|\bigcup_{i=1}^n A_i \right| = \sum_{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}} (-1)^{|J|-1}{\Biggl |}\bigcap_{j\in J}A_{j}{\Biggr |}$$

می‌خواهیم اثبات کنیم که هر عنصری که حداقل در یکی از مجموعه‌های $A_i$ وجود داشته باشد، در فرمول فقط یک بار شمرده می‌شود (توجه داشته باشید که عناصری که در هیچ‌یک از مجموعه‌های $A_i$ وجود ندارند، هرگز در سمت راست فرمول در نظر گرفته نمی‌شوند).

عنصر $x$ را در نظر بگیرید که در $k \geq 1$ مجموعه از $A_i$ها وجود دارد. نشان خواهیم داد که این عنصر فقط یک بار در فرمول شمرده می‌شود. توجه داشته باشید که:

  • در جملاتی که $|J| = 1$ است، عنصر $x$ به تعداد $+k$ بار شمرده می‌شود؛
  • در جملاتی که $|J| = 2$ است، عنصر $x$ به تعداد $-\binom{k}{2}$ بار شمرده می‌شود - زیرا در جملاتی شمارش می‌شود که شامل دو مجموعه از $k$ مجموعه‌ای هستند که $x$ را در خود دارند؛
  • در جملاتی که $|J| = 3$ است، عنصر $x$ به تعداد $+\binom{k}{3}$ بار شمرده می‌شود؛
  • $\cdots$
  • در جملاتی که $|J| = k$ است، عنصر $x$ به تعداد $(-1)^{k-1}\cdot \binom{k}{k}$ بار شمرده می‌شود؛
  • در جملاتی که $|J| > k$ است، عنصر $x$ به تعداد صفر بار شمرده می‌شود؛

این ما را به مجموع زیر از ضرایب دوجمله‌ای می‌رساند:

$$ T = \binom{k}{1} - \binom{k}{2} + \binom{k}{3} - \cdots + (-1)^{i-1}\cdot \binom{k}{i} + \cdots + (-1)^{k-1}\cdot \binom{k}{k}$$

این عبارت بسیار شبیه به بسط دوجمله‌ای $(1 - x)^k$ است:

$$ (1 - x)^k = \binom{k}{0} - \binom{k}{1} \cdot x + \binom{k}{2} \cdot x^2 - \binom{k}{3} \cdot x^3 + \cdots + (-1)^k\cdot \binom{k}{k} \cdot x^k $$

وقتی $x = 1$ باشد، $(1 - x)^k$ شباهت زیادی به $T$ دارد. با این حال، عبارت بسط یک جمله اضافی $\binom{k}{0} = 1$ دارد و کل عبارت در $-1$ ضرب شده است. این ما را به $(1 - 1)^k = 1 - T$ می‌رساند. بنابراین $T = 1 - (1 - 1)^k = 1$ است که همان چیزی بود که باید اثبات می‌شد. این عنصر فقط یک بار شمرده می‌شود.

تعمیم برای محاسبه تعداد عناصری که دقیقاً در r مجموعه قرار دارند

اصل شمول و طرد را می‌توان برای محاسبه تعداد عناصری که در هیچ مجموعه‌ای وجود ندارند، بازنویسی کرد:

$$\left|\bigcap_{i=1}^n \overline{A_i}\right|=\sum_{m=0}^n (-1)^m \sum_{|X|=m} \left|\bigcap_{i\in X} A_{i}\right|$$

تعمیم آن را برای محاسبه تعداد عناصری که دقیقاً در $r$ مجموعه وجود دارند، در نظر بگیرید:

$$\left|\bigcup_{|B|=r}\left[\bigcap_{i \in B} A_i \cap \bigcap_{j \not\in B} \overline{A_j}\right]\right|=\sum_{m=r}^n (-1)^{m-r}\dbinom{m}{r} \sum_{|X|=m} \left|\bigcap_{i \in X} A_{i}\right|$$

برای اثبات این فرمول، یک $B$ خاص را در نظر بگیرید. با استفاده از اصل پایه شمول و طرد می‌توان در مورد آن گفت:

$$\left|\bigcap_{i \in B} A_i \cap \bigcap_{j \not \in B} \overline{A_j}\right|=\sum_{m=r}^{n} (-1)^{m-r} \sum_{\substack{|X|=m \newline B \subset X}}\left|\bigcap_{i\in X} A_{i}\right|$$

مجموعه‌های سمت چپ برای $B$های مختلف اشتراک ندارند، بنابراین می‌توانیم آنها را مستقیماً با هم جمع کنیم. همچنین باید توجه داشت که هر مجموعه $X$ در صورت وقوع، همیشه ضریب $(-1)^{m-r}$ را خواهد داشت و دقیقاً برای $\dbinom{m}{r}$ مجموعه $B$ رخ می‌دهد.

کاربرد در حل مسائل

درک اصل شمول و طرد بدون مطالعه کاربردهای آن دشوار است.

ابتدا، سه مسئله ساده "روی کاغذ" را بررسی می‌کنیم که کاربردهای این اصل را نشان می‌دهند و سپس مسائل عملی‌تری را در نظر می‌گیریم که حل آنها بدون اصل شمول و طرد دشوار است.

مسائلی که می‌خواهند «تعداد راه‌ها» را پیدا کنید، قابل توجه هستند، زیرا گاهی اوقات به راه‌حل‌های چندجمله‌ای منجر می‌شوند، نه لزوماً نمایی.

یک مسئله ساده در مورد جایگشت‌ها

مسئله: تعداد جایگشت‌های اعداد ۰ تا ۹ را بشمارید که در آنها عنصر اول بزرگتر از ۱ و عنصر آخر کوچکتر از ۸ باشد.

بیایید تعداد جایگشت‌های «بد» را بشماریم، یعنی جایگشت‌هایی که در آنها عنصر اول $\leq 1$ و/یا عنصر آخر $\geq 8$ است.

مجموعه جایگشت‌هایی که عنصر اول آنها $\leq 1$ است را با $X$ و مجموعه جایگشت‌هایی که عنصر آخر آنها $\geq 8$ است را با $Y$ نشان می‌دهیم. آنگاه تعداد جایگشت‌های «بد»، طبق فرمول شمول و طرد، برابر خواهد بود با:

$$ |X \cup Y| = |X| + |Y| - |X \cap Y| $$

پس از یک محاسبه ترکیبیاتی ساده، به این نتیجه می‌رسیم:

$$ 2 \cdot 9! + 2 \cdot 9! - 2 \cdot 2 \cdot 8! $$

تنها کاری که باقی مانده این است که این عدد را از تعداد کل یعنی $!10$ کم کنیم تا تعداد جایگشت‌های «خوب» به دست آید.

یک مسئله ساده در مورد دنباله‌های (۰, ۱, ۲)

مسئله: تعداد دنباله‌هایی به طول $n$ که فقط از اعداد ۰، ۱ و ۲ تشکیل شده‌اند و هر عدد حداقل یک بار در آنها ظاهر می‌شود را بشمارید.

باز هم به مسئله معکوس روی می‌آوریم، یعنی تعداد دنباله‌هایی را محاسبه می‌کنیم که حداقل یکی از اعداد را ندارند.

مجموعه دنباله‌هایی که در آنها رقم $i$ ظاهر نمی‌شود را با $A_i (i = 0,1,2)$ نشان می‌دهیم. فرمول شمول و طرد برای تعداد دنباله‌های «بد» به این صورت خواهد بود:

$$ |A_0 \cup A_1 \cup A_2| = |A_0| + |A_1| + |A_2| - |A_0 \cap A_1| - |A_0 \cap A_2| - |A_1 \cap A_2| + |A_0 \cap A_1 \cap A_2| $$
  • اندازه هر $A_i$ برابر $2^n$ است، زیرا هر دنباله فقط می‌تواند شامل دو رقم از سه رقم باشد.
  • اندازه هر اشتراک دوتایی $A_i \cap A_j$ برابر با $1$ است، زیرا فقط یک رقم برای ساخت دنباله وجود خواهد داشت.
  • اندازه اشتراک هر سه مجموعه برابر با $0$ است، زیرا هیچ رقمی برای ساخت دنباله وجود نخواهد داشت.

از آنجایی که ما مسئله معکوس را حل کردیم، نتیجه را از تعداد کل دنباله‌ها یعنی $3^n$ کم می‌کنیم:

$$3^n - (3 \cdot 2^n - 3 \cdot 1 + 0)$$

تعداد جواب‌های صحیح معادلات با کران بالا

معادله زیر را در نظر بگیرید:

$$x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 20$$

که در آن $0 \le x_i \le 8 ~ (i = 1,2,\ldots 6)$ است.

مسئله: تعداد جواب‌های این معادله را بشمارید.

برای لحظه‌ای محدودیت روی $x_i$ را فراموش کنید و فقط تعداد جواب‌های نامنفی این معادله را بشمارید. این کار به راحتی با استفاده از روش ستاره و خط انجام می‌شود: می‌خواهیم دنباله‌ای از $20$ واحد را به $6$ گروه تقسیم کنیم، که معادل چیدن $5$ خط و $20$ ستاره است:

$$N_0 = \binom{25}{5}$$

اکنون تعداد جواب‌های «بد» را با اصل شمول و طرد محاسبه می‌کنیم. جواب‌های «بد» آنهایی هستند که در آنها یک یا چند $x_i$ بزرگتر یا مساوی $9$ باشند.

مجموعه جواب‌هایی که در آن $x_k \ge 9$ و بقیه $x_i \ge 0 ~ (i \ne k)$ هستند را با $A_k ~ (k = 1,2\ldots 6)$ نشان می‌دهیم (آنها ممکن است $\ge 9$ باشند یا نباشند). برای محاسبه اندازه $A_k$، توجه داشته باشید که اساساً با همان مسئله ترکیبیاتی روبرو هستیم که در دو پاراگراف بالا حل شد، اما اکنون $9$ واحد از کل واحدها کنار گذاشته شده و قطعاً به گروه اول تعلق دارند. بنابراین:

$$ | A_k | = \binom{16}{5} $$

به طور مشابه، اندازه اشتراک بین دو مجموعه $A_k$ و $A_p$ (برای $k \ne p$) برابر است با:

$$ \left| A_k \cap A_p \right| = \binom{7}{5}$$

اندازه هر اشتراک سه‌تایی از مجموعه‌ها صفر است، زیرا $20$ واحد برای اینکه سه یا چند متغیر بزرگتر یا مساوی $9$ باشند، کافی نخواهد بود.

با ترکیب همه اینها در فرمول شمول و طرد و با توجه به اینکه مسئله معکوس را حل کردیم، در نهایت به جواب می‌رسیم:

$$\binom{25}{5} - \left(\binom{6}{1} \cdot \binom{16}{5} - \binom{6}{2} \cdot \binom{7}{5}\right) $$

این روش به راحتی برای $d$ عدد که مجموعشان $s$ است با محدودیت $0 \le x_i \le b$ تعمیم می‌یابد:

$$\sum_{i=0}^d (-1)^i \binom{d}{i} \binom{s+d-1-(b+1)i}{d-1}$$

همانند بالا، ضرایب دوجمله‌ای با اندیس بالای منفی را صفر در نظر می‌گیریم.

توجه داشته باشید که این مسئله را می‌توان با برنامه‌نویسی پویا یا توابع مولد نیز حل کرد. پاسخ با استفاده از اصل شمول و طرد در زمان $O(d)$ محاسبه می‌شود (با فرض اینکه عملیات ریاضی مانند ضریب دوجمله‌ای در زمان ثابت انجام شوند)، در حالی که یک رویکرد ساده برنامه‌نویسی پویا (DP) زمان $O(ds)$ را می‌گیرد.

تعداد اعداد متباین در یک بازه معین

مسئله: با داشتن دو عدد $n$ و $r$، تعداد اعداد صحیح در بازه $[1;r]$ را که نسبت به n اول هستند (بزرگترین مقسوم‌علیه مشترکشان $1$ است)، بشمارید.

بیایید مسئله معکوس را حل کنیم - تعداد اعدادی که نسبت به $n$ اول نیستند را محاسبه کنیم.

عوامل اول $n$ را با $p_i (i = 1\cdots k)$ نشان می‌دهیم.

چند عدد در بازه $[1;r]$ بر $p_i$ بخش‌پذیر هستند؟ پاسخ این سوال این است:

$$ \left\lfloor \frac{ r }{ p_i } \right\rfloor $$

با این حال، اگر ما به سادگی این اعداد را جمع کنیم، برخی از اعداد چندین بار جمع زده می‌شوند (آنهایی که چندین $p_i$ را به عنوان عامل مشترک دارند). بنابراین، لازم است از اصل شمول و طرد استفاده کنیم.

ما روی تمام $2^k$ زیرمجموعه از $p_i$ها پیمایش می‌کنیم، حاصل‌ضرب آنها را محاسبه کرده و تعداد مضارب حاصل‌ضربشان را اضافه یا کم می‌کنیم.

در اینجا یک پیاده‌سازی با C++ آمده است:

int solve (int n, int r) {
    vector<int> p;
    for (int i=2; i*i<=n; ++i)
        if (n % i == 0) {
            p.push_back (i);
            while (n % i == 0)
                n /= i;
        }
    if (n > 1)
        p.push_back (n);

    int sum = 0;
    for (int msk=1; msk<(1<<p.size()); ++msk) {
        int mult = 1,
            bits = 0;
        for (int i=0; i<(int)p.size(); ++i)
            if (msk & (1<<i)) {
                ++bits;
                mult *= p[i];
            }

        int cur = r / mult;
        if (bits % 2 == 1)
            sum += cur;
        else
            sum -= cur;
    }

    return r - sum;
}

پیچیدگی زمانی این راه‌حل $O (\sqrt{n})$ است.

تعداد اعداد صحیح در یک بازه معین که مضرب حداقل یکی از اعداد داده شده هستند

$n$ عدد $a_i$ و یک عدد $r$ داده شده است. شما می‌خواهید تعداد اعداد صحیح در بازه $[1; r]$ را که مضرب حداقل یکی از $a_i$ها هستند، بشمارید.

الگوریتم راه‌حل تقریباً مشابه با مسئله قبلی است — فرمول شمول و طرد را بر روی اعداد $a_i$ بسازید، یعنی هر جمله در این فرمول تعداد اعدادی است که بر یک زیرمجموعه معین از اعداد $a_i$ بخش‌پذیر هستند (به عبارت دیگر، بر کوچکترین مضرب مشترک آنها بخش‌پذیرند).

بنابراین ما روی تمام $2^n$ زیرمجموعه از اعداد صحیح $a_i$ با $O(n \log r)$ عملیات برای یافتن کوچکترین مضرب مشترک آنها پیمایش می‌کنیم و تعداد مضارب آن را در بازه اضافه یا کم می‌کنیم. پیچیدگی زمانی $O (2^n\cdot n\cdot \log r)$ است.

تعداد رشته‌هایی که با یک الگوی معین مطابقت دارند

$n$ الگوی رشته‌ای با طول یکسان در نظر بگیرید که فقط از حروف ($a...z$) یا علامت سؤال تشکیل شده‌اند. یک عدد $k$ نیز به شما داده می‌شود. یک رشته با یک الگو مطابقت دارد اگر طول آن با الگو یکسان باشد و در هر موقعیت، یا کاراکترهای متناظر برابر باشند یا کاراکتر در الگو یک علامت سؤال باشد. مسئله این است که تعداد رشته‌هایی را بشمارید که دقیقاً با $k$ الگو (مسئله اول) و حداقل با $k$ الگو (مسئله دوم) مطابقت دارند.

ابتدا توجه کنید که می‌توانیم به راحتی تعداد رشته‌هایی را بشماریم که همزمان با همه الگوهای مشخص شده مطابقت دارند. برای این کار، کافی است الگوها را "ترکیب" کنیم: در طول موقعیت‌ها ("خانه‌ها") پیمایش کرده و یک موقعیت را در تمام الگوها بررسی کنید. اگر همه الگوها در این موقعیت علامت سؤال داشته باشند، کاراکتر می‌تواند هر حرفی از 'a' تا 'z' باشد. در غیر این صورت، کاراکتر این موقعیت به طور یکتا توسط الگوهایی که علامت سؤال ندارند، تعیین می‌شود.

حالا یاد بگیریم که نسخه اول مسئله را حل کنیم: زمانی که رشته باید دقیقاً با $k$ الگو مطابقت داشته باشد.

برای حل آن، یک زیرمجموعه خاص $X$ از مجموعه الگوها که شامل $k$ الگو است را پیمایش و ثابت می‌کنیم. سپس باید تعداد رشته‌هایی را بشماریم که با این مجموعه الگوها مطابقت دارند و فقط با همین مجموعه مطابقت دارند، یعنی با هیچ الگوی دیگری مطابقت ندارند. ما از اصل شمول و طرد به روشی کمی متفاوت استفاده خواهیم کرد: ما روی همه بالامجموعه‌های $Y$ (زیرمجموعه‌هایی از مجموعه اصلی رشته‌ها که شامل $X$ هستند) جمع می‌زنیم و یا به پاسخ فعلی اضافه می‌کنیم یا از تعداد رشته‌ها کم می‌کنیم:

$$ ans(X) = \sum_{Y \supseteq X} (-1)^{|Y|-k} \cdot f(Y) $$

که در آن $f(Y)$ تعداد رشته‌هایی است که با $Y$ (حداقل با $Y$) مطابقت دارند.

(اگر در فهمیدن این موضوع مشکل دارید، می‌توانید نمودارهای ون را رسم کنید.)

اگر روی تمام $ans(X)$ها جمع بزنیم، به پاسخ نهایی می‌رسیم:

$$ ans = \sum_{X ~ : ~ |X| = k} ans(X) $$

با این حال، پیچیدگی زمانی این راه‌حل $O(3^k \cdot k)$ است. برای بهبود آن، توجه کنید که محاسبات مختلف $ans(X)$ اغلب از مجموعه‌های $Y$ مشترکی استفاده می‌کنند.

ما فرمول شمول و طرد را معکوس کرده و بر حسب مجموعه‌های $Y$ جمع می‌زنیم. اکنون مشخص می‌شود که همان مجموعه $Y$ در محاسبه $ans(X)$ برای $\binom{|Y|}{k}$ مجموعه با علامت یکسان $(-1)^{|Y| - k}$ در نظر گرفته می‌شود.

$$ ans = \sum_{Y ~ : ~ |Y| \ge k} (-1)^{|Y|-k} \cdot \binom{|Y|}{k} \cdot f(Y) $$

حالا راه‌حل ما دارای پیچیدگی زمانی $O(2^k \cdot k)$ است.

اکنون نسخه دوم مسئله را حل می‌کنیم: تعداد رشته‌هایی را پیدا کنید که با حداقل $k$ الگو مطابقت دارند.

البته، می‌توانیم از راه‌حل نسخه اول مسئله استفاده کرده و پاسخ‌ها را برای مجموعه‌هایی با اندازه بزرگتر از $k$ جمع کنیم. با این حال، ممکن است متوجه شوید که در این مسئله، یک مجموعه |Y| در فرمول برای تمام مجموعه‌هایی با اندازه $\ge k$ که در $Y$ قرار دارند، در نظر گرفته می‌شود. به این ترتیب، می‌توانیم بخشی از عبارت را که در $f(Y)$ ضرب می‌شود، به صورت زیر بنویسیم:

$$ (-1)^{|Y|-k} \cdot \binom{|Y|}{k} + (-1)^{|Y|-k-1} \cdot \binom{|Y|}{k+1} + (-1)^{|Y|-k-2} \cdot \binom{|Y|}{k+2} + \cdots + (-1)^{|Y|-|Y|} \cdot \binom{|Y|}{|Y|} $$

با نگاهی به کتاب "ریاضیات گسسته" گراهام (Graham, Knuth, Patashnik. "Concrete mathematics" [1998])، یک فرمول شناخته شده برای ضرایب دوجمله‌ای را می‌بینیم:

$$ \sum_{k=0}^m (-1)^k \cdot \binom{n}{k} = (-1)^m \cdot \binom{n-1}{m} $$

با اعمال آن در اینجا، متوجه می‌شویم که کل مجموع ضرایب دوجمله‌ای ساده می‌شود:

$$ (-1)^{|Y|-k} \cdot \binom{|Y|-1}{|Y|-k} $$

بنابراین، برای این مسئله نیز، ما یک راه‌حل با پیچیدگی زمانی $O(2^k \cdot k)$ به دست آوردیم:

$$ ans = \sum_{Y ~ : ~ |Y| \ge k} (-1)^{|Y|-k} \cdot \binom{|Y|-1}{|Y|-k} \cdot f(Y) $$

تعداد راه‌های رفتن از یک سلول به سلول دیگر

یک زمین $n \times m$ وجود دارد و $k$ سلول آن دیوارهای غیرقابل عبور هستند. یک ربات در ابتدا در سلول $(1,1)$ (پایین سمت چپ) قرار دارد. ربات فقط می‌تواند به سمت راست یا بالا حرکت کند و در نهایت باید به سلول $(n,m)$ برسد و از همه موانع اجتناب کند. شما باید تعداد راه‌هایی را که او می‌تواند این کار را انجام دهد، بشمارید.

فرض کنید که اندازه‌های $n$ و $m$ بسیار بزرگ هستند (مثلاً $10^9$) و تعداد $k$ کوچک است (حدود $100$).

ابتدا، موانع را بر اساس مختصات $x$ آنها و در صورت تساوی، بر اساس مختصات $y$ مرتب کنید.

همچنین یاد بگیرید چگونه یک مسئله بدون مانع را حل کنید: یعنی یاد بگیرید چگونه تعداد راه‌های رسیدن از یک سلول به سلول دیگر را بشمارید. در یک محور، باید از $x$ سلول عبور کنیم و در محور دیگر، از $y$ سلول. از ترکیبیات ساده، فرمولی با استفاده از ضرایب دوجمله‌ای به دست می‌آوریم:

$$\binom{x+y}{x}$$

حالا برای شمارش تعداد راه‌های رسیدن از یک سلول به سلول دیگر با اجتناب از همه موانع، می‌توانید از اصل شمول و طرد برای حل مسئله معکوس استفاده کنید: تعداد راه‌های عبور از روی یک زیرمجموعه از موانع را بشمارید (و آن را از تعداد کل راه‌ها کم کنید).

هنگام پیمایش یک زیرمجموعه از موانع که از روی آنها عبور خواهیم کرد، برای شمارش تعداد راه‌های انجام این کار، کافی است تعداد تمام مسیرها از سلول شروع به اولین مانع انتخاب شده، از اولین مانع به دومین مانع و به همین ترتیب را در هم ضرب کنید و سپس این عدد را مطابق با فرمول استاندارد شمول و طرد از پاسخ اضافه یا کم کنید.

با این حال، این راه‌حل دوباره با پیچیدگی غیرچندجمله‌ای $O(2^k \cdot k)$ خواهد بود.

در اینجا یک راه‌حل چندجمله‌ای ارائه می‌شود:

ما از برنامه‌نویسی پویا استفاده خواهیم کرد. برای راحتی، $(1,1)$ را به ابتدای آرایه موانع و $(n,m)$ را به انتهای آن اضافه می‌کنیم. بیایید اعداد $d[i]$ را محاسبه کنیم — تعداد راه‌های رسیدن از نقطه شروع (مانع صفرم) به مانع $i$-ام، بدون عبور از هیچ مانع دیگری (به جز خود مانع $i$-ام، البته). ما این عدد را برای تمام سلول‌های مانع و همچنین برای سلول پایانی محاسبه خواهیم کرد.

برای محاسبه $d[i]$ (تعداد مسیرهای معتبر به $i$)، تعداد کل مسیرها از 0 به $i$ را در نظر گرفته و مسیرهای «بد» را از آن کم می‌کنیم. یک مسیر بد، مسیری است که از حداقل یک مانع دیگر $j$ (که $x_j \le x_i$ و $y_j \le y_i$) عبور کند. برای هر مانع $j$ که قبل از $i$ قرار دارد، تعداد مسیرهایی که از ۰ به $i$ می‌روند و اولین مانعی که با آن برخورد می‌کنند $j$ است، برابر است با $d[j]$ (تعداد مسیرهای معتبر از ۰ تا $j$) ضربدر تعداد کل مسیرها از $j$ تا $i$. با جمع کردن این مقادیر برای تمام $j$ های ممکن و کم کردن آن از تعداد کل مسیرهای ۰ تا $i$، مقدار $d[i]$ به دست می‌آید.

ما می‌توانیم $d[i]$ را در $O(k)$ برای $O(k)$ مانع محاسبه کنیم، بنابراین این راه‌حل دارای پیچیدگی $O(k^2)$ است.

تعداد چهارتایی‌های متباین

$n$ عدد به شما داده شده است: $a_1, a_2, \ldots, a_n$. از شما خواسته شده تعداد راه‌های انتخاب چهار عدد را بشمارید به طوری که بزرگترین مقسوم‌علیه مشترک آنها برابر با یک باشد.

ما مسئله معکوس را حل می‌کنیم — تعداد چهارتایی‌های «بد» را محاسبه می‌کنیم، یعنی چهارتایی‌هایی که در آنها همه اعداد بر عددی $d > 1$ بخش‌پذیر هستند.

ما از اصل شمول و طرد استفاده می‌کنیم و بر روی تمام گروه‌های چهارتایی ممکن از اعداد که بر مقسوم‌علیه $d$ بخش‌پذیرند، جمع می‌زنیم.

$$ans = \sum_{d \ge 2} (-1)^{deg(d)-1} \cdot f(d)$$

که در آن $deg(d)$ تعداد عوامل اول در تجزیه عدد $d$ و $f(d)$ تعداد چهارتایی‌های بخش‌پذیر بر $d$ است.

برای محاسبه تابع $f(d)$، کافی است تعداد مضارب $d$ را بشمارید (همانطور که در یک مسئله قبلی ذکر شد) و از ضرایب دوجمله‌ای برای شمارش تعداد راه‌های انتخاب چهار عدد از آنها استفاده کنید.

بنابراین، با استفاده از فرمول شمول و طرد، ما تعداد گروه‌های چهارتایی بخش‌پذیر بر یک عدد اول را جمع می‌کنیم، سپس تعداد چهارتایی‌هایی را که بر حاصل‌ضرب دو عدد اول بخش‌پذیرند کم می‌کنیم، چهارتایی‌های بخش‌پذیر بر سه عدد اول را اضافه می‌کنیم و الی آخر.

تعداد سه‌تایی‌های هارمونیک

یک عدد $n \le 10^6$ به شما داده شده است. از شما خواسته شده تعداد سه‌تایی‌های $2 \le a < b < c \le n$ را بشمارید که یکی از شرایط زیر را برآورده کنند:

  • یا ${\rm gcd}(a,b) = {\rm gcd}(a,c) = {\rm gcd}(b,c) = 1$
  • یا ${\rm gcd}(a,b) > 1, {\rm gcd}(a,c) > 1, {\rm gcd}(b,c) > 1$

ابتدا، مستقیماً به سراغ مسئله معکوس می‌رویم — یعنی تعداد سه‌تایی‌های ناهماهنگ را می‌شماریم.

دوم، توجه داشته باشید که هر سه‌تایی ناهماهنگ از یک زوج متباین و یک عدد سوم تشکیل شده که با حداقل یکی از اعضای آن زوج، متباین نیست.

بنابراین، تعداد سه‌تایی‌های ناهماهنگ که شامل $i$ هستند، برابر است با تعداد اعداد صحیح از ۲ تا $n$ که نسبت به $i$ اول هستند ضربدر تعداد اعداد صحیحی که نسبت به $i$ اول نیستند.

یا $gcd(a,b) = 1 \wedge gcd(a,c) > 1 \wedge gcd(b,c) > 1$

یا $gcd(a,b) = 1 \wedge gcd(a,c) = 1 \wedge gcd(b,c) > 1$

در هر دو حالت، سه‌تایی دو بار شمرده می‌شود. حالت اول وقتی $i = a$ و وقتی $i = b$ شمرده می‌شود. حالت دوم وقتی $i = b$ و وقتی $i = c$ شمرده می‌شود. بنابراین، برای محاسبه تعداد سه‌تایی‌های ناهماهنگ، این محاسبه را برای تمام $i$ از ۲ تا $n$ جمع کرده و بر ۲ تقسیم می‌کنیم.

حالا تنها چیزی که برای حل باقی مانده، یادگیری شمارش تعداد اعداد متباین با $i$ در بازه $[2;n]$ است. اگرچه این مسئله قبلاً ذکر شده است، راه‌حل بالا در اینجا مناسب نیست — نیاز به تجزیه هر یک از اعداد صحیح از ۲ تا $n$ و سپس پیمایش تمام زیرمجموعه‌های این اعداد اول دارد.

یک راه‌حل سریع‌تر با چنین تغییری در غربال اراتستن امکان‌پذیر است:

  1. ابتدا، تمام اعدادی را در بازه $[2;n]$ پیدا می‌کنیم که تجزیه ساده آنها شامل یک عامل اول به صورت تکراری نباشد. همچنین باید بدانیم که این اعداد شامل چند عامل اول هستند.

    • برای این کار، یک آرایه $deg[i]$ برای ذخیره تعداد عوامل اول در تجزیه $i$ و یک آرایه $good[i]$ برای علامت‌گذاری اینکه آیا $i$ هر عامل را حداکثر یک بار شامل می‌شود ($good[i] = 1$) یا نه ($good[i] = 0$) نگهداری می‌کنیم. هنگام پیمایش از ۲ تا $n$، اگر به عددی برسیم که $deg$ آن برابر با ۰ باشد، آنگاه آن عدد اول است و $deg$ آن ۱ است.
    • در طول غربال اراتستن، ما $i$ را از ۲ تا $n$ پیمایش می‌کنیم. هنگام پردازش یک عدد اول، از تمام مضارب آن عبور کرده و $deg[]$ آنها را افزایش می‌دهیم. اگر یکی از این مضارب، مضرب مربع $i$ باشد، آنگاه می‌توانیم $good$ را false قرار دهیم.

  2. دوم، باید پاسخ را برای تمام $i$ از ۲ تا $n$ محاسبه کنیم، یعنی آرایه $cnt[]$ — تعداد اعداد صحیحی که نسبت به $i$ اول نیستند.

    • برای این کار، به یاد بیاورید که فرمول شمول و طرد چگونه کار می‌کند — در واقع در اینجا ما همان مفهوم را با منطق معکوس پیاده‌سازی می‌کنیم: ما روی یک مؤلفه (حاصل‌ضرب عوامل اول از تجزیه) پیمایش می‌کنیم و جمله آن را در فرمول شمول و طرد هر یک از مضاربش اضافه یا کم می‌کنیم.
    • بنابراین، فرض کنید ما در حال پردازش عددی $i$ هستیم که $good[i] = true$ است، یعنی در فرمول شمول و طرد نقش دارد. روی تمام اعدادی که مضرب $i$ هستند پیمایش کنید و $\lfloor N/i \rfloor$ را به $cnt[]$ آنها اضافه یا از آن کم کنید (علامت به $deg[i]$ بستگی دارد: اگر $deg[i]$ فرد باشد، باید اضافه کنیم، در غیر این صورت کم کنیم).

در اینجا یک پیاده‌سازی با C++ آمده است:

int n;
bool good[MAXN];
int deg[MAXN], cnt[MAXN];

long long solve() {
    memset (good, 1, sizeof good);
    memset (deg, 0, sizeof deg);
    memset (cnt, 0, sizeof cnt);

    long long ans_bad = 0;
    for (int i=2; i<=n; ++i) {
        if (good[i]) {
            if (deg[i] == 0)  deg[i] = 1;
            for (int j=1; i*j<=n; ++j) {
                if (j > 1 && deg[i] == 1)
                    if (j % i == 0)
                        good[i*j] = false;
                    else
                        ++deg[i*j];
                cnt[i*j] += (n / i) * (deg[i]%2==1 ? +1 : -1);
            }
        }
        ans_bad += (cnt[i] - 1) * 1ll * (n-1 - cnt[i]);
    }

    return (n-1) * 1ll * (n-2) * (n-3) / 6 - ans_bad / 2;
}

پیچیدگی زمانی راه‌حل ما $O(n \log n)$ است، زیرا تقریباً برای هر عدد تا $n$ ما $n/i$ تکرار در حلقه تودرتو انجام می‌دهیم.

تعداد جایگشت‌های بدون نقطه ثابت (پریش‌ها)

اثبات کنید که تعداد جایگشت‌های طول $n$ بدون نقطه ثابت (یعنی هیچ عدد $i$ در موقعیت $i$ قرار ندارد - که به آن پریش (derangement) نیز گفته می‌شود) برابر است با عدد زیر:

$$n! - \binom{n}{1} \cdot (n-1)! + \binom{n}{2} \cdot (n-2)! - \binom{n}{3} \cdot (n-3)! + \cdots \pm \binom{n}{n} \cdot (n-n)! $$

و تقریباً برابر است با:

$$ \frac{ n! }{ e } $$

(اگر این عبارت را به نزدیک‌ترین عدد صحیح گرد کنید — دقیقاً تعداد جایگشت‌های بدون نقطه ثابت را به دست می‌آورید)

مجموعه جایگشت‌های طول $n$ با یک نقطه ثابت در موقعیت $k$ ($1 \le k \le n$) (یعنی عنصر $k$ در موقعیت $k$ قرار دارد) را با $A_k$ نشان می‌دهیم.

اکنون از فرمول شمول و طرد برای شمارش تعداد جایگشت‌های با حداقل یک نقطه ثابت استفاده می‌کنیم. برای این کار باید یاد بگیریم اندازه‌های اشتراک مجموعه‌های $A_i$ را به صورت زیر بشماریم:

$$\begin{eqnarray} \left| A_p \right| &=& (n-1)!\ , \\ \left| A_p \cap A_q \right| &=& (n-2)!\ , \\ \left| A_p \cap A_q \cap A_r \right| &=& (n-3)!\ , \\ \cdots , \end{eqnarray}$$

زیرا اگر بدانیم تعداد نقاط ثابت برابر با $x$ است، آنگاه موقعیت $x$ عنصر از جایگشت را می‌دانیم و تمام $(n-x)$ عنصر دیگر می‌توانند در هر جایی قرار گیرند.

با جایگزینی این در فرمول شمول و طرد، و با توجه به اینکه تعداد راه‌های انتخاب یک زیرمجموعه به اندازه $x$ از مجموعه $n$ عنصری برابر با $\binom{n}{x}$ است، فرمولی برای تعداد جایگشت‌های با حداقل یک نقطه ثابت به دست می‌آوریم:

$$\binom{n}{1} \cdot (n-1)! - \binom{n}{2} \cdot (n-2)! + \binom{n}{3} \cdot (n-3)! - \cdots \pm \binom{n}{n} \cdot (n-n)! $$

سپس تعداد جایگشت‌های بدون نقطه ثابت برابر است با:

$$n! - \binom{n}{1} \cdot (n-1)! + \binom{n}{2} \cdot (n-2)! - \binom{n}{3} \cdot (n-3)! + \cdots \pm \binom{n}{n} \cdot (n-n)! $$

با ساده‌سازی این عبارت، عبارات دقیق و تقریبی برای تعداد جایگشت‌های بدون نقطه ثابت را به دست می‌آوریم:

$$ n! \left( 1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots \pm \frac{1}{n!} \right ) \approx \frac{n!}{e} $$

(زیرا مجموع داخل پرانتز، $n+1$ جمله اول بسط سری تیلور $e^{-1}$ است)

شایان ذکر است که مسئله مشابهی را می‌توان به این روش حل کرد: زمانی که نیاز است نقاط ثابت در میان $m$ عنصر اول جایگشت‌ها نباشند (و نه در میان همه، همانطور که ما حل کردیم). فرمول به دست آمده مانند فرمول دقیق بالا خواهد بود، اما تا مجموع $k$ ادامه خواهد یافت، به جای $n$.

مسائل تمرینی

لیستی از مسائلی که می‌توان با استفاده از اصل شمول و طرد حل کرد: