دومین درخت پوشای کمینه¶
یک درخت پوشای کمینه (Minimum Spanning Tree) $T$ برای یک گراف دادهشدهی $G$ درختی است که تمام رئوس گراف را پوشش میدهد و از بین تمام درختهای پوشای ممکن، کمترین مجموع وزن یالها را دارد. یک دومین درخت پوشای کمینه $T'$، درخت پوشایی است که از بین تمام درختهای پوشای ممکن برای گراف $G$، دومین مجموع وزن کمینه را در بین یالهایش دارد.
مشاهده¶
فرض کنید $T$ درخت پوشای کمینه گراف $G$ باشد. میتوان مشاهده کرد که دومین درخت پوشای کمینه با درخت پوشای کمینه ($T$) فقط در یک یال تفاوت دارد. (برای اثبات این گزاره، به مسئلهی ۱-۲۳ اینجا مراجعه کنید).
بنابراین، باید یالی مانند $e_{new}$ را پیدا کنیم که در $T$ وجود ندارد و آن را با یک یال از $T$ (فرض کنید $e_{old}$) جایگزین کنیم، به طوری که گراف جدید $T' = (T \cup \{e_{new}\}) \setminus \{e_{old}\}$ یک درخت پوشا باشد و اختلاف وزن ($e_{new} - e_{old}$) کمینه شود.
استفاده از الگوریتم کراسکال¶
میتوانیم ابتدا با استفاده از الگوریتم کراسکال، درخت پوشای کمینه (MST) را پیدا کنیم و سپس تلاش کنیم هر بار یک یال از آن را حذف کرده و با یال دیگری جایگزین کنیم.
- یالها را در زمان $O(E \log E)$ مرتب کرده، سپس با استفاده از الگوریتم کراسکال در زمان $O(E)$ یک MST پیدا کنید.
- به ازای هر یال موجود در MST (که $V-1$ یال خواهد داشت)، آن را به طور موقت از لیست یالها خارج کنید تا نتواند انتخاب شود.
- سپس، با استفاده از یالهای باقیمانده، دوباره در زمان $O(E)$ یک MST پیدا کنید.
- این کار را برای تمام یالهای موجود در MST تکرار کرده و بهترین نتیجه را از بین همه انتخاب کنید.
توجه: نیازی به مرتبسازی دوبارهی یالها در مرحله ۳ نیست.
بنابراین، پیچیدگی زمانی کلی برابر با $O(E \log V + E + V E)$ = $O(V E)$ خواهد بود.
مدلسازی به مسئلهی پایینترین جد مشترک (LCA)¶
در رویکرد قبلی، تمام حالتهای ممکن برای حذف یک یال از MST را امتحان کردیم. در اینجا دقیقاً برعکس عمل خواهیم کرد. سعی میکنیم هر یالی را که از قبل در MST وجود ندارد، اضافه کنیم.
- یالها را در زمان $O(E \log E)$ مرتب کرده، سپس با استفاده از الگوریتم کراسکال در زمان $O(E)$ یک MST پیدا کنید.
- به ازای هر یال $e$ که در MST وجود ندارد، آن را به طور موقت به MST اضافه کنید تا یک دور ایجاد شود. این دور از LCA عبور خواهد کرد.
- یال $k$ با بیشترین وزن را در این دور پیدا کنید که با $e$ برابر نباشد. این کار با دنبال کردن والدین رئوس یال $e$ تا رسیدن به LCA انجام میشود.
- یال $k$ را به طور موقت حذف کنید تا یک درخت پوشای جدید ایجاد شود.
- اختلاف وزن $\delta = weight(e) - weight(k)$ را محاسبه کرده و آن را به همراه یال تغییریافته به خاطر بسپارید.
- مرحله ۲ را برای تمام یالهای دیگر تکرار کنید و درخت پوشایی را که کمترین اختلاف وزن را با MST دارد، برگردانید.
پیچیدگی زمانی الگوریتم به نحوهی محاسبهی $k$ها بستگی دارد، که همان یالهای با بیشترین وزن در مرحله ۲ این الگوریتم هستند. یک راه برای محاسبهی بهینهی آنها در زمان $O(E \log V)$، تبدیل مسئله به یک مسئلهی پایینترین جد مشترک (LCA) است.
ما با ریشهدار کردن MST، مسئلهی LCA را پیشپردازش میکنیم و همچنین بیشترین وزن یالها را برای هر رأس در مسیر به سمت اجدادش محاسبه خواهیم کرد. این کار را میتوان با استفاده از پرش دودویی (Binary Lifting) برای LCA انجام داد.
پیچیدگی زمانی نهایی این رویکرد $O(E \log V)$ است.
برای مثال:
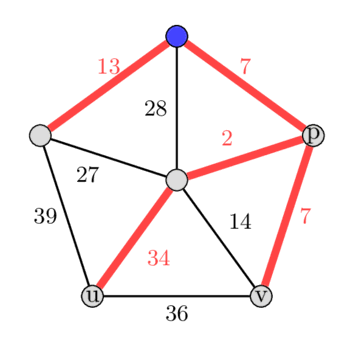
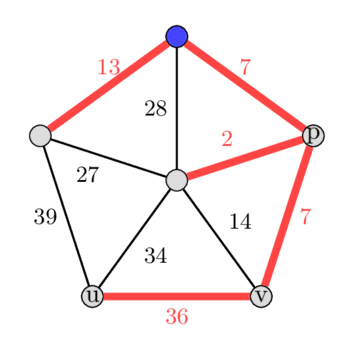
*در تصویر، سمت چپ MST و سمت راست دومین MST کمینه است.*
در گراف دادهشده، فرض کنید MST را در رأس آبیرنگ بالا ریشهدار کنیم، و سپس الگوریتم خود را با انتخاب یالهایی که در MST نیستند، اجرا کنیم. فرض کنید اولین یال انتخابشده، یال $(u, v)$ با وزن ۳۶ باشد. اضافه کردن این یال به درخت، یک دور به صورت ۳۶ - ۷ - ۲ - ۳۴ ایجاد میکند.
حالا با پیدا کردن $\text{LCA}(u, v) = p$، یال با بیشترین وزن را در این دور پیدا میکنیم. ما یال با بیشترین وزن را در مسیرهای از $u$ به $p$ و از $v$ به $p$ محاسبه میکنیم. توجه: در برخی موارد، $\text{LCA}(u, v)$ میتواند با $u$ یا $v$ برابر باشد. در این مثال، یال با وزن ۳۴ به عنوان یال با بیشترین وزن در دور به دست میآید. با حذف این یال، یک درخت پوشای جدید به دست میآوریم که اختلاف وزنی برابر با تنها ۲ واحد دارد.
پس از انجام این کار برای تمام یالهای دیگری که بخشی از MST اولیه نیستند، میبینیم که این درخت پوشا، در کل دومین درخت پوشای کمینه نیز بوده است. انتخاب یال با وزن ۱۴، وزن درخت را ۷ واحد افزایش میدهد، انتخاب یال با وزن ۲۷ آن را ۱۴ واحد افزایش میدهد، انتخاب یال با وزن ۲۸ آن را ۲۱ واحد افزایش میدهد و انتخاب یال با وزن ۳۹، وزن درخت را ۵ واحد افزایش میدهد.
پیادهسازی¶
struct edge {
int s, e, w, id;
bool operator<(const struct edge& other) { return w < other.w; }
};
typedef struct edge Edge;
const int N = 2e5 + 5;
long long res = 0, ans = 1e18;
int n, m, a, b, w, id, l = 21;
vector<Edge> edges;
vector<int> h(N, 0), parent(N, -1), size(N, 0), present(N, 0);
vector<vector<pair<int, int>>> adj(N), dp(N, vector<pair<int, int>>(l));
vector<vector<int>> up(N, vector<int>(l, -1));
pair<int, int> combine(pair<int, int> a, pair<int, int> b) {
vector<int> v = {a.first, a.second, b.first, b.second};
int topTwo = -3, topOne = -2;
for (int c : v) {
if (c > topOne) {
topTwo = topOne;
topOne = c;
} else if (c > topTwo && c < topOne) {
topTwo = c;
}
}
return {topOne, topTwo};
}
void dfs(int u, int par, int d) {
h[u] = 1 + h[par];
up[u][0] = par;
dp[u][0] = {d, -1};
for (auto v : adj[u]) {
if (v.first != par) {
dfs(v.first, u, v.second);
}
}
}
pair<int, int> lca(int u, int v) {
pair<int, int> ans = {-2, -3};
if (h[u] < h[v]) {
swap(u, v);
}
for (int i = l - 1; i >= 0; i--) {
if (h[u] - h[v] >= (1 << i)) {
ans = combine(ans, dp[u][i]);
u = up[u][i];
}
}
if (u == v) {
return ans;
}
for (int i = l - 1; i >= 0; i--) {
if (up[u][i] != -1 && up[v][i] != -1 && up[u][i] != up[v][i]) {
ans = combine(ans, combine(dp[u][i], dp[v][i]));
u = up[u][i];
v = up[v][i];
}
}
ans = combine(ans, combine(dp[u][0], dp[v][0]));
return ans;
}
int main(void) {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
for (int i = 1; i <= m; i++) {
cin >> a >> b >> w; // اندیسگذاری از ۱
edges.push_back({a, b, w, i - 1});
}
sort(edges.begin(), edges.end());
for (int i = 0; i <= m - 1; i++) {
a = edges[i].s;
b = edges[i].e;
w = edges[i].w;
id = edges[i].id;
if (unite_set(a, b)) {
adj[a].emplace_back(b, w);
adj[b].emplace_back(a, w);
present[id] = 1;
res += w;
}
}
dfs(1, 0, 0);
for (int i = 1; i <= l - 1; i++) {
for (int j = 1; j <= n; ++j) {
if (up[j][i - 1] != -1) {
int v = up[j][i - 1];
up[j][i] = up[v][i - 1];
dp[j][i] = combine(dp[j][i - 1], dp[v][i - 1]);
}
}
}
for (int i = 0; i <= m - 1; i++) {
id = edges[i].id;
w = edges[i].w;
if (!present[id]) {
auto rem = lca(edges[i].s, edges[i].e);
if (rem.first != w) {
if (ans > res + w - rem.first) {
ans = res + w - rem.first;
}
} else if (rem.second != -1) {
if (ans > res + w - rem.second) {
ans = res + w - rem.second;
}
}
}
}
cout << ans << "\n";
return 0;
}
منابع¶
- Competitive Programming-3، نوشتهی Steven Halim
- web.mit.edu