درخت پوشای کمینه - الگوریتم کراسکال¶
یک گراف وزندار و بدون جهت داده شده است. میخواهیم یک زیردرخت از این گراف را پیدا کنیم که همهی رأسها را به هم متصل کند (یعنی یک درخت پوشا باشد) و کمترین وزن ممکن را داشته باشد (یعنی مجموع وزنهای تمام یالهای آن در بین تمام درختهای پوشای ممکن، کمینه باشد). این درخت پوشا، «درخت پوشای کمینه» (minimum spanning tree) نامیده میشود.
در تصویر سمت چپ میتوانید یک گراف وزندار و بدون جهت را ببینید و در تصویر سمت راست، درخت پوشای کمینه متناظر با آن نمایش داده شده است.
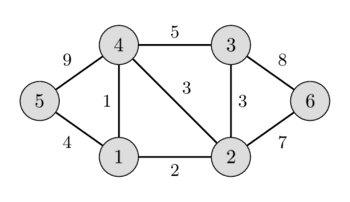
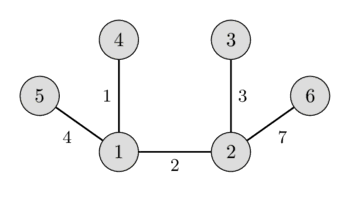
این مقاله چند حقیقت مهم مرتبط با درختان پوشای کمینه را بررسی میکند و سپس سادهترین پیادهسازی الگوریتم کراسکال برای یافتن درخت پوشای کمینه را ارائه میدهد.
ویژگیهای درخت پوشای کمینه¶
- یک درخت پوشای کمینه از یک گراف، در صورتی که وزن تمام یالها متمایز باشد، یکتا است. در غیر این صورت، ممکن است چندین درخت پوشای کمینه وجود داشته باشد. (الگوریتمهای خاص معمولاً یکی از درختان پوشای کمینه ممکن را خروجی میدهند).
- درخت پوشای کمینه، درختی با کمترین حاصلضرب وزن یالها نیز هست. (این موضوع را میتوان به راحتی با جایگزین کردن وزن تمام یالها با لگاریتم آنها اثبات کرد).
- در یک درخت پوشای کمینه از یک گراف، بیشترین وزن یک یال، کمترین مقدار ممکن از بین تمام درختان پوشای آن گراف است. (این نتیجه از درستی الگوریتم کراسکال به دست میآید).
- درخت پوشای بیشینه (درخت پوشایی که مجموع وزن یالهای آن بیشینه باشد) از یک گراف را میتوان مشابه درخت پوشای کمینه به دست آورد؛ کافی است علامت وزن تمام یالها را معکوس کرده و سپس هر یک از الگوریتمهای درخت پوشای کمینه را اعمال کنیم.
الگوریتم کراسکال¶
این الگوریتم توسط جوزف برنارد کراسکال جونیور در سال ۱۹۵۶ توصیف شد.
الگوریتم کراسکال در ابتدا تمام رأسهای گراف اصلی را به صورت جدا از هم قرار میدهد تا جنگلی از درختان تکرأسی تشکیل دهد. سپس به تدریج این درختان را با هم ادغام میکند و در هر مرحله، دو درخت دلخواه را با استفاده از یکی از یالهای گراف اصلی ترکیب میکند. قبل از اجرای الگوریتم، تمام یالها بر اساس وزن (به ترتیب غیرنزولی) مرتب میشوند. سپس فرآیند ادغام آغاز میشود: تمام یالها را از اولین تا آخرین (به ترتیب مرتبشده) انتخاب میکنیم و اگر دو سر یال انتخابشده به زیردرختهای متفاوتی تعلق داشته باشند، این زیردرختها با هم ترکیب شده و یال به جواب اضافه میشود. پس از پیمایش تمام یالها، همه رأسها به یک زیردرخت واحد تعلق خواهند داشت و ما به جواب میرسیم.
سادهترین پیادهسازی¶
کد زیر مستقیماً الگوریتم توصیفشده در بالا را پیادهسازی میکند و دارای پیچیدگی زمانی $O(M \log M + N^2)$ است.
مرتبسازی یالها به $O(M \log N)$ (که همان $O(M \log M)$ است) عملیات نیاز دارد.
اطلاعات مربوط به زیردرختی که یک رأس به آن تعلق دارد، با کمک آرایهی tree_id[] نگهداری میشود - برای هر رأس v، tree_id[v] شمارهی درختی را که v به آن تعلق دارد، ذخیره میکند.
برای هر یال، اینکه آیا دو سر آن به درختان متفاوتی تعلق دارند یا نه، در زمان $O(1)$ قابل تشخیص است.
در نهایت، ادغام دو درخت با یک پیمایش ساده روی آرایهی tree_id[] در $O(N)$ انجام میشود.
با توجه به اینکه تعداد کل عملیات ادغام $N-1$ است، به پیچیدگی زمانی $O(M \log N + N^2)$ میرسیم.
struct Edge {
int u, v, weight;
bool operator<(Edge const& other) {
return weight < other.weight;
}
};
int n;
vector<Edge> edges;
int cost = 0;
vector<int> tree_id(n);
vector<Edge> result;
for (int i = 0; i < n; i++)
tree_id[i] = i;
sort(edges.begin(), edges.end());
for (Edge e : edges) {
if (tree_id[e.u] != tree_id[e.v]) {
cost += e.weight;
result.push_back(e);
int old_id = tree_id[e.u], new_id = tree_id[e.v];
for (int i = 0; i < n; i++) {
if (tree_id[i] == old_id)
tree_id[i] = new_id;
}
}
}
اثبات درستی¶
چرا الگوریتم کراسکال نتیجهی درستی به ما میدهد؟
اگر گراف اولیه همبند باشد، گراف حاصل نیز همبند خواهد بود. زیرا در غیر این صورت، دو مؤلفه وجود خواهند داشت که میتوانستند با حداقل یک یال به هم متصل شوند. اما این غیرممکن است، زیرا کراسکال یکی از این یالها را انتخاب میکرد، چون شناسهی مؤلفههای آنها متفاوت است. همچنین گراف حاصل هیچ دوری ندارد، زیرا ما صریحاً این موضوع را در الگوریتم منع کردهایم. بنابراین، الگوریتم یک درخت پوشا تولید میکند.
پس چرا این الگوریتم یک درخت پوشای کمینه به ما میدهد؟
میتوانیم گزاره «اگر $F$ مجموعهای از یالهای انتخابشده توسط الگوریتم در هر مرحله باشد، آنگاه یک درخت پوشای کمینه (MST) وجود دارد که شامل تمام یالهای $F$ است» را با استقرا ثابت کنیم.
این گزاره در ابتدا بدیهتاً درست است؛ مجموعهی تهی زیرمجموعهای از هر MST است.
حال فرض کنیم $F$ مجموعهی یالها در یک مرحله از الگوریتم باشد، $T$ یک MST شامل $F$ باشد و $e$ یال جدیدی باشد که میخواهیم با استفاده از کراسکال اضافه کنیم.
اگر $e$ یک دور ایجاد کند، آن را اضافه نمیکنیم، بنابراین گزاره پس از این مرحله همچنان درست است.
در صورتی که $T$ از قبل شامل $e$ باشد، گزاره پس از این مرحله نیز درست است.
در صورتی که $T$ شامل یال $e$ نباشد، آنگاه $T + e$ شامل یک دور $C$ خواهد بود. این دور حداقل شامل یک یال $f$ خواهد بود که در $F$ نیست. مجموعه یالهای $T - f + e$ نیز یک درخت پوشا خواهد بود. توجه داشته باشید که وزن $f$ نمیتواند کمتر از وزن $e$ باشد، زیرا در غیر این صورت کراسکال زودتر $f$ را انتخاب میکرد. همچنین وزن آن نمیتواند بیشتر باشد، زیرا این امر باعث میشود وزن کل $T - f + e$ کمتر از وزن کل $T$ شود، که غیرممکن است چون $T$ از قبل یک MST است. این بدان معناست که وزن $e$ باید با وزن $f$ برابر باشد. بنابراین $T - f + e$ نیز یک MST است و شامل تمام یالهای $F + e$ میباشد. پس در اینجا نیز گزاره پس از این مرحله همچنان برقرار است.
این اثبات، درستی گزاره را نشان میدهد. این یعنی پس از پیمایش تمام یالها، مجموعهی یال حاصل همبند خواهد بود و در یک MST وجود خواهد داشت، که به این معناست که خود آن مجموعه باید یک MST باشد.
پیادهسازی بهبودیافته¶
میتوانیم از ساختمان داده Disjoint Set Union (DSU) برای نوشتن پیادهسازی سریعتری از الگوریتم کراسکال با پیچیدگی زمانی حدود $O(M \log N)$ استفاده کنیم. این مقاله چنین رویکردی را با جزئیات شرح میدهد.
مسائل تمرینی¶
- SPOJ - Koicost
- SPOJ - MaryBMW
- Codechef - Fullmetal Alchemist
- Codeforces - Edges in MST
- UVA 12176 - Bring Your Own Horse
- UVA 10600 - ACM Contest and Blackout
- UVA 10724 - Road Construction
- Hackerrank - Roads in HackerLand
- UVA 11710 - Expensive subway
- Codechef - Chefland and Electricity
- UVA 10307 - Killing Aliens in Borg Maze
- Codeforces - Flea
- Codeforces - Igon in Museum
- Codeforces - Hongcow Builds a Nation
- UVA - 908 - Re-connecting Computer Sites
- UVA 1208 - Oreon
- UVA 1235 - Anti Brute Force Lock
- UVA 10034 - Freckles
- UVA 11228 - Transportation system
- UVA 11631 - Dark roads
- UVA 11733 - Airports
- UVA 11747 - Heavy Cycle Edges
- SPOJ - Blinet
- SPOJ - Help the Old King
- Codeforces - Hierarchy
- SPOJ - Modems
- CSES - Road Reparation
- CSES - Road Construction