حل RMQ (Range Minimum Query) با یافتن LCA (Lowest Common Ancestor)¶
آرایهی A[0..N-1] داده شده است.
به ازای هر پرس و جو (query) به فرم [L, R]، میخواهیم کمینه را در آرایهی A از خانهی L تا خانهی R پیدا کنیم.
فرض میکنیم که آرایهی A در طول این فرآیند تغییر نمیکند، یعنی این مقاله یک راه حل برای مسئلهی RMQ ایستا (static) را شرح میدهد.
در اینجا شرح یک راه حل بهینهی مجانبی ارائه میشود. این راه حل از دیگر راه حلهای مسئلهی RMQ متمایز است، زیرا رویکردی بسیار متفاوت دارد: این روش مسئلهی RMQ را به مسئلهی LCA کاهش میدهد، و سپس از الگوریتم Farach-Colton and Bender استفاده میکند، که خود این الگوریتم مسئلهی LCA را دوباره به یک مسئلهی RMQ خاص کاهش داده و آن را حل میکند.
الگوریتم¶
ما یک درخت دکارتی (Cartesian tree) از آرایهی A میسازیم.
درخت دکارتی یک آرایهی A، یک درخت دودویی با خاصیت min-heap است (مقدار گره والد باید کوچکتر یا مساوی مقدار گرههای فرزندش باشد) به طوری که پیمایش میانترتیب (in-order) درخت، گرهها را به همان ترتیبی که در آرایهی A قرار دارند، ملاقات میکند.
به عبارت دیگر، درخت دکارتی یک ساختمان دادهی بازگشتی است.
آرایهی A به ۳ بخش تقسیم میشود: پیشوند آرایه تا عنصر کمینه، خود عنصر کمینه، و پسوند باقیمانده.
ریشهی درخت، گرهای متناظر با عنصر کمینهی آرایهی A خواهد بود، زیردرخت چپ، درخت دکارتی پیشوند خواهد بود، و زیردرخت راست، درخت دکارتی پسوند خواهد بود.
در تصویر زیر میتوانید یک آرایه به طول ۱۰ و درخت دکارتی متناظر با آن را ببینید.
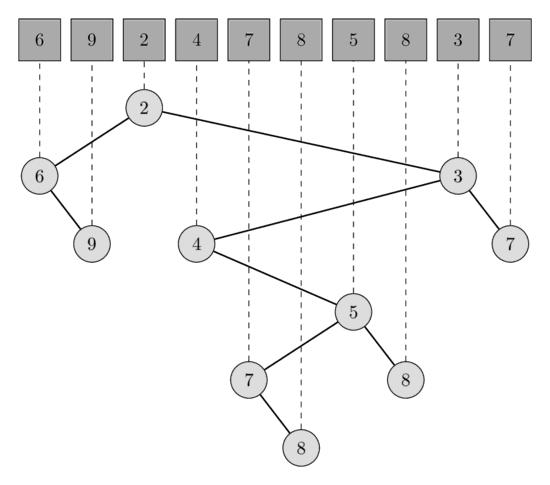
پرس و جوی کمینه در بازه [l, r] معادل با پرس و جوی پایینترین جد مشترک [l', r'] است، که در آن l' گره متناظر با عنصر A[l] و r' گره متناظر با عنصر A[r] است.
در واقع، گره متناظر با کوچکترین عنصر در بازه باید جد تمام گرههای آن بازه باشد، و در نتیجه جد l' و r' نیز هست.
این موضوع به طور خودکار از خاصیت min-heap نتیجه میشود.
و همچنین باید پایینترین جد باشد، زیرا در غیر این صورت l' و r' هر دو در زیردرخت چپ یا هر دو در زیردرخت راست قرار میگرفتند، که این امر منجر به تناقض میشود، زیرا در چنین حالتی، عنصر کمینه اصلاً در بازهی مورد نظر قرار نمیگرفت.
در تصویر زیر میتوانید پرس و جوهای LCA را برای پرس و جوهای RMQ [1, 3] و [5, 9] مشاهده کنید.
در پرس و جوی اول، LCA گرههای A[1] و A[3]، گره متناظر با A[2] است که مقدار ۲ را دارد، و در پرس و جوی دوم، LCA گرههای A[5] و A[9]، گره متناظر با A[8] است که مقدار ۳ را دارد.
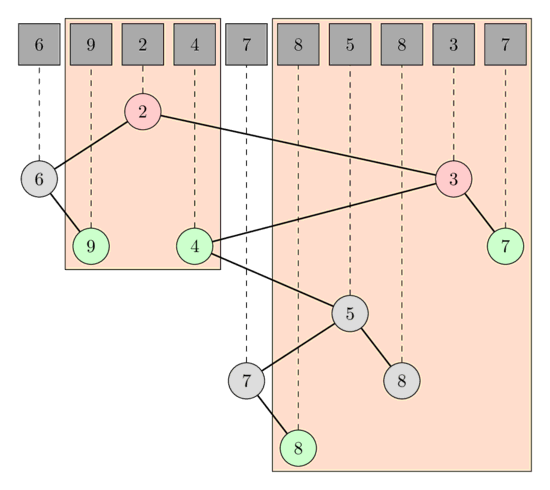
چنین درختی را میتوان در زمان $O(N)$ ساخت و الگوریتم Farach-Colton and Benders میتواند درخت را در $O(N)$ پیشپردازش کند و LCA را در $O(1)$ بیابد.
ساخت درخت دکارتی¶
ما درخت دکارتی را با اضافه کردن عناصر یکی پس از دیگری خواهیم ساخت.
در هر مرحله، ما یک درخت دکارتی معتبر از تمام عناصر پردازش شده را حفظ میکنیم.
به راحتی میتوان دید که اضافه کردن یک عنصر s[i] فقط میتواند گرههای موجود در راستترین مسیر درخت را تغییر دهد - مسیری که از ریشه شروع شده و به طور مکرر فرزند راست انتخاب میشود.
زیردرختِ گرهای با کوچکترین مقداری که بزرگتر یا مساوی s[i] است، به زیردرخت چپِ s[i] تبدیل میشود، و درختی که ریشهاش s[i] است، به عنوان زیردرخت راست جدیدِ گرهای با بزرگترین مقداری که کوچکتر از s[i] است، قرار میگیرد.
این کار را میتوان با استفاده از یک پشته (stack) برای ذخیرهی اندیسهای گرههای راستترین مسیر پیادهسازی کرد.
vector<int> parent(n, -1);
stack<int> s;
for (int i = 0; i < n; i++) {
int last = -1;
while (!s.empty() && A[s.top()] >= A[i]) {
last = s.top();
s.pop();
}
if (!s.empty())
parent[i] = s.top();
if (last >= 0)
parent[last] = i;
s.push(i);
}