2-SAT¶
مسئله صدقپذیری بولی (SAT) مسئلهای است که در آن به متغیرها مقادیر بولی (صحیح یا غلط) نسبت داده میشود تا یک فرمول بولی دادهشده برقرار شود. فرمول بولی معمولاً به شکل CNF (فرم عطفی نرمال) داده میشود که عبارت است از عطف (AND) چندین گزاره (clause)، که در آن هر گزاره، فصل (OR) چند لیترال (متغیرها یا نقیض آنها) است. مسئله 2-SAT (۲-صدقپذیری) محدودیتی از مسئله SAT است. در 2-SAT، هر گزاره دقیقاً دو لیترال دارد. در اینجا مثالی از یک مسئله 2-SAT آورده شده است. مقداری برای $a, b, c$ بیابید که فرمول زیر صحیح باشد:
مسئله SAT از نوع NP-کامل است و هیچ راهحل کارآمدی برای آن شناخته نشده است. اما 2-SAT را میتوان به طور کارآمد در زمان $O(n + m)$ حل کرد که در آن $n$ تعداد متغیرها و $m$ تعداد گزارهها است.
الگوریتم¶
ابتدا باید مسئله را به فرم دیگری تبدیل کنیم که به آن فرم استلزام عطفی میگویند. توجه داشته باشید که عبارت $a \lor b$ معادل است با $\lnot a \Rightarrow b \land \lnot b \Rightarrow a$ (اگر یکی از دو متغیر غلط باشد، دیگری باید حتماً صحیح باشد).
اکنون یک گراف جهتدار از این استلزامها میسازیم: برای هر متغیر $x$، دو رأس $v_x$ و $v_{\lnot x}$ وجود خواهد داشت. یالهای گراف متناظر با استلزامها هستند.
بیایید به مثال در فرم 2-CNF نگاه کنیم:
گراف جهتدار شامل رئوس و یالهای زیر خواهد بود:
میتوانید گراف استلزام را در تصویر زیر ببینید:
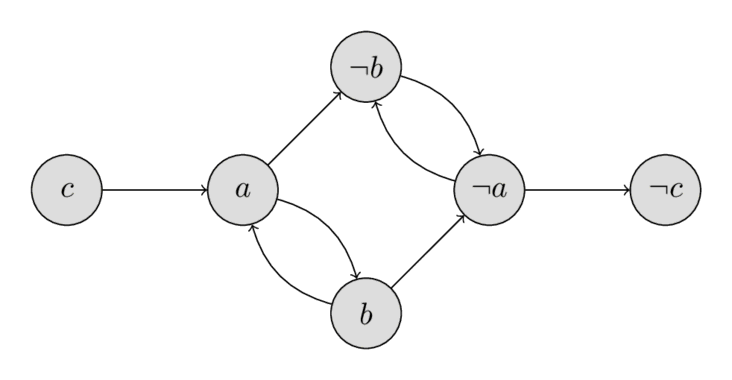
شایان ذکر است که به این ویژگی گراف استلزام توجه کنیم: اگر یالی از $a$ به $b$ وجود داشته باشد ($a \Rightarrow b$)، آنگاه یالی از $\lnot b$ به $\lnot a$ نیز وجود دارد.
همچنین توجه داشته باشید که اگر $x$ از $\lnot x$ قابلدسترسی باشد و $\lnot x$ نیز از $x$ قابلدسترسی باشد، مسئله راهحل ندارد. هر مقداری که برای متغیر $x$ انتخاب کنیم، به تناقض میرسیم - اگر $x$ مقدار $\text{true}$ بگیرد، استلزام به ما میگوید که $\lnot x$ نیز باید $\text{true}$ باشد و بالعکس. مشخص میشود که این شرط نه تنها لازم، بلکه کافی نیز هست. این موضوع را در چند پاراگراف بعدی اثبات خواهیم کرد. ابتدا به یاد بیاورید که اگر یک رأس از رأس دوم قابلدسترسی باشد و رأس دوم نیز از رأس اول قابلدسترسی باشد، این دو رأس در یک مؤلفه قویاً همبند قرار دارند. بنابراین، میتوانیم شرط وجود راهحل را به صورت زیر فرمولبندی کنیم:
برای اینکه مسئله 2-SAT راهحل داشته باشد، شرط لازم و کافی این است که برای هر متغیر $x$، رئوس $x$ و $\lnot x$ در مؤلفههای قویاً همبند متفاوتی از گراف استلزام قرار داشته باشند.
این شرط را میتوان در زمان $O(n + m)$ با یافتن تمام مؤلفههای قویاً همبند بررسی کرد.
تصویر زیر تمام مؤلفههای قویاً همبند را برای مثال نشان میدهد. همانطور که به راحتی میتوان بررسی کرد، هیچیک از چهار مؤلفه شامل یک رأس $x$ و نقیض آن $\lnot x$ نیست، بنابراین مثال راهحل دارد. در پاراگرافهای بعدی یاد خواهیم گرفت که چگونه یک جواب معتبر را محاسبه کنیم، اما صرفاً برای نمایش، راهحل $a = \text{false}$، $b = \text{false}$، $c = \text{false}$ ارائه شده است.
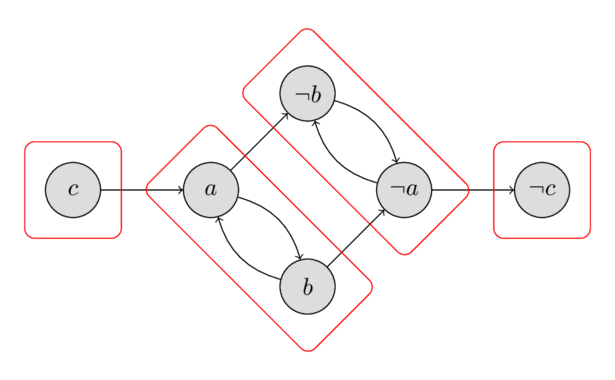
اکنون الگوریتمی برای یافتن راهحل مسئله 2-SAT با این فرض که راهحل وجود دارد، میسازیم.
توجه داشته باشید که با وجود اینکه راهحل وجود دارد، ممکن است در گراف استلزام، $\lnot x$ از $x$ قابلدسترسی باشد، یا (اما نه همزمان) $x$ از $\lnot x$ قابلدسترسی باشد. در این حالت، انتخاب یکی از مقادیر $\text{true}$ یا $\text{false}$ برای $x$ به تناقض منجر میشود، در حالی که انتخاب مقدار دیگر چنین نیست. بیایید یاد بگیریم چگونه مقداری را انتخاب کنیم که به تناقض نرسیم.
بیایید مؤلفههای قویاً همبند را به ترتیب توپولوژیک مرتب کنیم (یعنی اگر مسیری از $v$ به $u$ وجود داشته باشد، آنگاه $\text{comp}[v] \le \text{comp}[u]$) و فرض کنیم $\text{comp}[v]$ اندیس مؤلفه قویاً همبندی را نشان میدهد که رأس $v$ به آن تعلق دارد. سپس، اگر $\text{comp}[x] < \text{comp}[\lnot x]$ باشد، به $x$ مقدار $\text{false}$ و در غیر این صورت مقدار $\text{true}$ را اختصاص میدهیم.
بیایید اثبات کنیم که با این مقداردهی متغیرها به تناقض نمیرسیم. فرض کنید به $x$ مقدار $\text{true}$ اختصاص داده شده است. حالت دیگر را میتوان به روشی مشابه اثبات کرد.
ابتدا اثبات میکنیم که رأس $x$ نمیتواند به رأس $\lnot x$ برسد. چون ما مقدار $\text{true}$ را اختصاص دادیم، باید اندیس مؤلفه قویاً همبند $x$ بزرگتر از اندیس مؤلفه $\lnot x$ باشد. این بدان معناست که $\lnot x$ در سمت چپ مؤلفهای قرار دارد که شامل $x$ است و رأس دوم ($x$) نمیتواند به رأس اول ($\lnot x$) برسد.
دوم، اثبات میکنیم که متغیری مانند $y$ وجود ندارد که رئوس $y$ و $\lnot y$ هر دو از $x$ در گراف استلزام قابلدسترسی باشند. این امر باعث تناقض میشود، زیرا $x = \text{true}$ ایجاب میکند که $y = \text{true}$ و $\lnot y = \text{true}$ باشد. این را با برهان خلف اثبات میکنیم. فرض کنید $y$ و $\lnot y$ هر دو از $x$ قابلدسترسی هستند، در این صورت با توجه به ویژگی گراف استلزام، $\lnot x$ از هر دوی $y$ و $\lnot y$ قابلدسترسی است. با خاصیت تعدی، نتیجه میشود که $\lnot x$ از $x$ قابلدسترسی است که این با فرض اولیه ما در تناقض است.
بنابراین ما الگوریتمی ساختیم که مقادیر مورد نیاز متغیرها را با این فرض پیدا میکند که برای هر متغیر $x$، رئوس $x$ و $\lnot x$ در مؤلفههای قویاً همبند متفاوتی قرار دارند. در بالا درستی این الگوریتم را نشان دادیم. در نتیجه، به طور همزمان معیار فوق برای وجود راهحل را نیز اثبات کردیم.
پیادهسازی¶
اکنون میتوانیم کل الگوریتم را پیادهسازی کنیم. ابتدا گراف استلزام را میسازیم و تمام مؤلفههای قویاً همبند را پیدا میکنیم. این کار را میتوان با الگوریتم کوساراجو در زمان $O(n + m)$ انجام داد. در پیمایش دوم گراف، الگوریتم کوساراجو مؤلفههای قویاً همبند را به ترتیب توپولوژیک پیمایش میکند، بنابراین محاسبه $\text{comp}[v]$ برای هر رأس $v$ آسان است.
پس از آن، میتوانیم مقداردهی $x$ را با مقایسه $\text{comp}[x]$ و $\text{comp}[\lnot x]$ انتخاب کنیم. اگر $\text{comp}[x] = \text{comp}[\lnot x]$ باشد، مقدار $\text{false}$ را برمیگردانیم تا نشان دهیم که هیچ مقداردهی معتبری که مسئله 2-SAT را ارضا کند وجود ندارد.
در زیر، پیادهسازی راهحل مسئله 2-SAT برای گراف استلزام از قبل ساختهشده $adj$ و گراف معکوس (ترانهاده) $adj^{\intercal}$ (که در آن جهت هر یال برعکس شده است) آمده است. در این گراف، رئوس با اندیسهای $2k$ و $2k+1$ دو رأس متناظر با متغیر $k$ هستند که $2k+1$ متناظر با متغیر نقیض شده است.
struct TwoSatSolver {
int n_vars;
int n_vertices;
vector<vector<int>> adj, adj_t;
vector<bool> used;
vector<int> order, comp;
vector<bool> assignment;
TwoSatSolver(int _n_vars) : n_vars(_n_vars), n_vertices(2 * n_vars), adj(n_vertices), adj_t(n_vertices), used(n_vertices), order(), comp(n_vertices, -1), assignment(n_vars) {
order.reserve(n_vertices);
}
void dfs1(int v) {
used[v] = true;
for (int u : adj[v]) {
if (!used[u])
dfs1(u);
}
order.push_back(v);
}
void dfs2(int v, int cl) {
comp[v] = cl;
for (int u : adj_t[v]) {
if (comp[u] == -1)
dfs2(u, cl);
}
}
bool solve_2SAT() {
order.clear();
used.assign(n_vertices, false);
for (int i = 0; i < n_vertices; ++i) {
if (!used[i])
dfs1(i);
}
comp.assign(n_vertices, -1);
for (int i = 0, j = 0; i < n_vertices; ++i) {
int v = order[n_vertices - i - 1];
if (comp[v] == -1)
dfs2(v, j++);
}
assignment.assign(n_vars, false);
for (int i = 0; i < n_vertices; i += 2) {
if (comp[i] == comp[i + 1])
return false;
assignment[i / 2] = comp[i] > comp[i + 1];
}
return true;
}
void add_disjunction(int a, bool na, int b, bool nb) {
// na و nb مشخص میکنند که آیا a و b باید نقیض شوند یا خیر
a = 2 * a ^ na;
b = 2 * b ^ nb;
int neg_a = a ^ 1;
int neg_b = b ^ 1;
adj[neg_a].push_back(b);
adj[neg_b].push_back(a);
adj_t[b].push_back(neg_a);
adj_t[a].push_back(neg_b);
}
static void example_usage() {
TwoSatSolver solver(3); // متغیرهای a, b, c
solver.add_disjunction(0, false, 1, true); // a v not b
solver.add_disjunction(0, true, 1, true); // not a v not b
solver.add_disjunction(1, false, 2, false); // b v c
solver.add_disjunction(0, false, 0, false); // a v a
assert(solver.solve_2SAT() == true);
auto expected = vector<bool>(True, False, True);
assert(solver.assignment == expected);
}
};