مکانیابی نقطه در $O(log n)$¶
مسئله زیر را در نظر بگیرید: به شما یک planar subdivision (افراز صفحهای) بدون هیچ رأسی با درجه یک و صفر و تعداد زیادی پرسوجو (query) داده شده است.
هر پرسوجو یک نقطه است که برای آن باید مشخص کنیم به کدام وجه (face) از افراز تعلق دارد.
ما به هر پرسوجو به صورت آفلاین (offline) و در زمان $O(\log n)$ پاسخ خواهیم داد.
این مسئله ممکن است زمانی پیش بیاید که شما نیاز به مکانیابی چند نقطه در یک دیاگرام ورونوی (Voronoi diagram) یا در یک چندضلعی ساده داشته باشید.
الگوریتم¶
ابتدا، برای هر نقطه پرسوجوی $p\ (x_0, y_0)$، میخواهیم یالی را پیدا کنیم که اگر نقطه به یالی تعلق داشته باشد، نقطه روی همان یال پیدا شده قرار گیرد. در غیر این صورت، این یال باید خط $x = x_0$ را در نقطهای یکتای $(x_0, y)$ قطع کند، به طوری که $y < y_0$ باشد و این $y$ در میان تمام چنین یالهایی بیشینه باشد. تصویر زیر هر دو حالت را نشان میدهد.
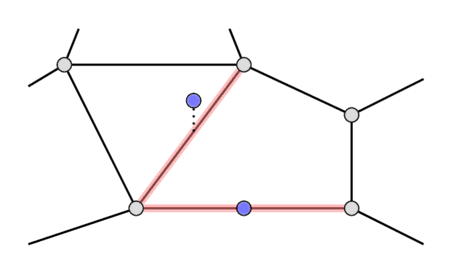
ما این مسئله را به صورت آفلاین (offline) با استفاده از الگوریتم خط جاروب (sweep line) حل خواهیم کرد. بیایید روی مختصات x نقاط پرسوجو و نقاط پایانی یالها به ترتیب صعودی پیمایش کنیم و یک مجموعه از یالها به نام $s$ را نگهداری کنیم. برای هر مختصات x، از قبل چند رویداد (event) اضافه خواهیم کرد.
رویدادها از چهار نوع خواهند بود: add (افزودن)، remove (حذف)، vertical (عمودی) و get (دریافت). برای هر یال عمودی (که هر دو نقطه انتهایی آن مختصات x یکسانی دارند)، یک رویداد vertical برای مختصات x مربوطه اضافه میکنیم. برای هر یال دیگر، یک رویداد add برای کمینه مختصات x نقاط انتهایی و یک رویداد remove برای بیشینه مختصات x نقاط انتهایی اضافه میکنیم. در نهایت، برای هر نقطه پرسوجو، یک رویداد get برای مختصات x آن اضافه میکنیم.
برای هر مختصات x، رویدادها را بر اساس نوعشان به ترتیب (vertical، get، remove، add) مرتب میکنیم. تصویر زیر تمام رویدادها را به ترتیب مرتبشده برای هر مختصات x نشان میدهد.
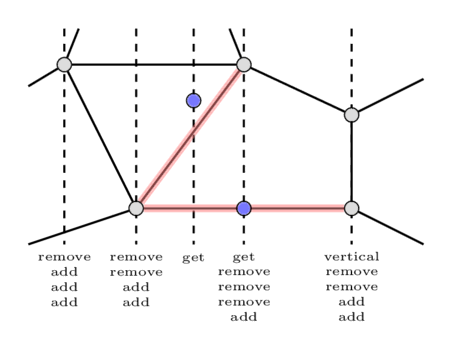
در طول فرآیند خط جاروب، دو مجموعه را نگهداری خواهیم کرد. یک مجموعه $t$ برای تمام یالهای غیرعمودی، و یک مجموعه $vert$ مخصوص یالهای عمودی. مجموعه $vert$ را در ابتدای پردازش هر مختصات x خالی خواهیم کرد.
اکنون رویدادها را برای یک مختصات x ثابت پردازش میکنیم.
- اگر با یک رویداد vertical مواجه شدیم، به سادگی کمینه مختصات y نقاط پایانی یال مربوطه را در $vert$ درج میکنیم.
- اگر با یک رویداد remove یا add مواجه شدیم، یال مربوطه را از $t$ حذف یا به آن اضافه میکنیم.
- در نهایت، برای هر رویداد get، باید با انجام یک جستجوی دودویی در $vert$ بررسی کنیم که آیا نقطه روی یک یال عمودی قرار دارد یا خیر. اگر نقطه روی هیچ یال عمودی قرار نداشت، باید پاسخ این پرسوجو را در $t$ پیدا کنیم. برای این کار، مجدداً یک جستجوی دودویی انجام میدهیم. برای مدیریت برخی موارد خاص (degenerate cases) (مثلاً در مورد مثلث $(0,~0)$، $(0,~2)$، $(1, 1)$ هنگامی که از نقطه $(0,~0)$ پرسوجو میکنیم)، باید پس از پردازش تمام رویدادهای مربوط به این مختصات x، دوباره به تمام رویدادهای get پاسخ دهیم و بهترین گزینه را از بین دو پاسخ انتخاب کنیم.
اکنون یک مقایسهگر (comparator) برای مجموعه $t$ انتخاب میکنیم.
این مقایسهگر ترتیب عمودی دو یال را تعیین میکند. فرض کنید دو یال $(a, b)$ و $(c, d)$ داریم. آنگاه مقایسهگر (در شبهکد) به صورت زیر است:
$val = sgn((b - a)\times(c - a)) + sgn((b - a)\times(d - a))$
اگر $val \neq 0$
آنگاه برگردان $val > 0$
$val = sgn((d - c)\times(a - c)) + sgn((d - c)\times(b - c))$
برگردان $val < 0$
اکنون برای هر پرسوجو، یال متناظر آن را در اختیار داریم. چگونه وجه را پیدا کنیم؟ اگر نتوانستیم یالی پیدا کنیم، به این معنی است که نقطه در وجه بیرونی قرار دارد. اگر نقطه به یال پیدا شده تعلق داشته باشد، وجه یکتا نیست. در غیر این صورت، دو گزینه وجود دارد - وجههایی که توسط این یال محدود شدهاند. چگونه بررسی کنیم کدام یک پاسخ است؟ توجه داشته باشید که این یال عمودی نیست. در این صورت، پاسخ، وجهی است که بالای این یال قرار دارد. بیایید برای هر یال غیرعمودی چنین وجهی را پیدا کنیم. یک پیمایش پادساعتگرد روی هر وجه را در نظر بگیرید. اگر در طول این پیمایش، هنگام عبور از یک یال، مختصات x افزایش یابد، آنگاه آن وجه، همان وجهی است که برای آن یال به دنبالش هستیم.
نکات¶
در واقع، با استفاده از درختهای پایا (persistent trees)، این رویکرد را میتوان برای پاسخ به پرسوجوها به صورت آنلاین (online) نیز به کار برد.
پیادهسازی¶
کد زیر برای اعداد صحیح پیادهسازی شده است، اما با تغییر متدهای مقایسه و نوع نقطه، میتوان آن را به راحتی برای کار با اعداد اعشاری (doubles) نیز تغییر داد.
این پیادهسازی فرض میکند که افراز به درستی در یک ساختار DCEL (لیست یالهای با اتصال دوگانه) ذخیره شده و وجه بیرونی با شماره ۱- مشخص شده است.
برای هر پرسوجو، اگر نقطه کاملاً داخل وجه شماره $i$ قرار داشته باشد، یک زوج $(1, i)$ برگردانده میشود، و اگر نقطه روی یال شماره $i$ قرار داشته باشد، یک زوج $(0, i)$ برگردانده میشود.
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& x) { return le(x, 0) ? eq(x, 0) ? 0 : -1 : 1; }
struct pt {
ll x, y;
pt() {}
pt(ll _x, ll _y) : x(_x), y(_y) {}
pt operator-(const pt& a) const { return pt(x - a.x, y - a.y); }
ll dot(const pt& a) const { return x * a.x + y * a.y; }
ll dot(const pt& a, const pt& b) const { return (a - *this).dot(b - *this); }
ll cross(const pt& a) const { return x * a.y - y * a.x; }
ll cross(const pt& a, const pt& b) const { return (a - *this).cross(b - *this); }
bool operator==(const pt& a) const { return a.x == x && a.y == y; }
};
struct Edge {
pt l, r;
};
bool edge_cmp(Edge* edge1, Edge* edge2)
{
const pt a = edge1->l, b = edge1->r;
const pt c = edge2->l, d = edge2->r;
int val = sgn(a.cross(b, c)) + sgn(a.cross(b, d));
if (val != 0)
return val > 0;
val = sgn(c.cross(d, a)) + sgn(c.cross(d, b));
return val < 0;
}
enum EventType { DEL = 2, ADD = 3, GET = 1, VERT = 0 };
struct Event {
EventType type;
int pos;
bool operator<(const Event& event) const { return type < event.type; }
};
vector<Edge*> sweepline(vector<Edge*> planar, vector<pt> queries)
{
using pt_type = decltype(pt::x);
// جمعآوری تمام مختصات x
auto s =
set<pt_type, std::function<bool(const pt_type&, const pt_type&)>>(lt);
for (pt p : queries)
s.insert(p.x);
for (Edge* e : planar) {
s.insert(e->l.x);
s.insert(e->r.x);
}
// نگاشت تمام مختصات x به شناسهها
int cid = 0;
auto id =
map<pt_type, int, std::function<bool(const pt_type&, const pt_type&)>>(
lt);
for (auto x : s)
id[x] = cid++;
// ایجاد رویدادها
auto t = set<Edge*, decltype(*edge_cmp)>(edge_cmp);
auto vert_cmp = [](const pair<pt_type, int>& l,
const pair<pt_type, int>& r) {
if (!eq(l.first, r.first))
return lt(l.first, r.first);
return l.second < r.second;
};
auto vert = set<pair<pt_type, int>, decltype(vert_cmp)>(vert_cmp);
vector<vector<Event>> events(cid);
for (int i = 0; i < (int)queries.size(); i++) {
int x = id[queries[i].x];
events[x].push_back(Event{GET, i});
}
for (int i = 0; i < (int)planar.size(); i++) {
int lx = id[planar[i]->l.x], rx = id[planar[i]->r.x];
if (lx > rx) {
swap(lx, rx);
swap(planar[i]->l, planar[i]->r);
}
if (lx == rx) {
events[lx].push_back(Event{VERT, i});
} else {
events[lx].push_back(Event{ADD, i});
events[rx].push_back(Event{DEL, i});
}
}
// اجرای الگوریتم خط جاروب
vector<Edge*> ans(queries.size(), nullptr);
for (int x = 0; x < cid; x++) {
sort(events[x].begin(), events[x].end());
vert.clear();
for (Event event : events[x]) {
if (event.type == DEL) {
t.erase(planar[event.pos]);
}
if (event.type == VERT) {
vert.insert(make_pair(
min(planar[event.pos]->l.y, planar[event.pos]->r.y),
event.pos));
}
if (event.type == ADD) {
t.insert(planar[event.pos]);
}
if (event.type == GET) {
auto jt = vert.upper_bound(
make_pair(queries[event.pos].y, planar.size()));
if (jt != vert.begin()) {
--jt;
int i = jt->second;
if (ge(max(planar[i]->l.y, planar[i]->r.y),
queries[event.pos].y)) {
ans[event.pos] = planar[i];
continue;
}
}
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
if (it != t.begin())
ans[event.pos] = *(--it);
delete e;
}
}
for (Event event : events[x]) {
if (event.type != GET)
continue;
if (ans[event.pos] != nullptr &&
eq(ans[event.pos]->l.x, ans[event.pos]->r.x))
continue;
Edge* e = new Edge;
e->l = e->r = queries[event.pos];
auto it = t.upper_bound(e);
delete e;
if (it == t.begin())
e = nullptr;
else
e = *(--it);
if (ans[event.pos] == nullptr) {
ans[event.pos] = e;
continue;
}
if (e == nullptr)
continue;
if (e == ans[event.pos])
continue;
if (id[ans[event.pos]->r.x] == x) {
if (id[e->l.x] == x) {
if (gt(e->l.y, ans[event.pos]->r.y))
ans[event.pos] = e;
}
} else {
ans[event.pos] = e;
}
}
}
return ans;
}
struct DCEL {
struct Edge {
pt origin;
Edge* nxt = nullptr;
Edge* twin = nullptr;
int face;
};
vector<Edge*> body;
};
vector<pair<int, int>> point_location(DCEL planar, vector<pt> queries)
{
vector<pair<int, int>> ans(queries.size());
vector<Edge*> planar2;
map<intptr_t, int> pos;
map<intptr_t, int> added_on;
int n = planar.body.size();
for (int i = 0; i < n; i++) {
if (planar.body[i]->face > planar.body[i]->twin->face)
continue;
Edge* e = new Edge;
e->l = planar.body[i]->origin;
e->r = planar.body[i]->twin->origin;
added_on[(intptr_t)e] = i;
pos[(intptr_t)e] =
lt(planar.body[i]->origin.x, planar.body[i]->twin->origin.x)
? planar.body[i]->face
: planar.body[i]->twin->face;
planar2.push_back(e);
}
auto res = sweepline(planar2, queries);
for (int i = 0; i < (int)queries.size(); i++) {
if (res[i] == nullptr) {
ans[i] = make_pair(1, -1);
continue;
}
pt p = queries[i];
pt l = res[i]->l, r = res[i]->r;
if (eq(p.cross(l, r), 0) && le(p.dot(l, r), 0)) {
ans[i] = make_pair(0, added_on[(intptr_t)res[i]]);
continue;
}
ans[i] = make_pair(1, pos[(intptr_t)res[i]]);
}
for (auto e : planar2)
delete e;
return ans;
}