پیدا کردن مماسهای مشترک دو دایره¶
دو دایره داده شده است. میخواهیم تمام مماسهای مشترک آنها را پیدا کنیم، یعنی تمام خطوطی که هر دو دایره را به طور همزمان لمس میکنند.
الگوریتم توصیف شده در حالتی که یک (یا هر دو) دایره به نقطه تبدیل شوند (حالت تبهگن) نیز کار میکند. بنابراین، از این الگوریتم میتوان برای پیدا کردن مماسهای یک دایره که از یک نقطه مشخص میگذرند نیز استفاده کرد.
تعداد مماسهای مشترک¶
تعداد مماسهای مشترک دو دایره میتواند ۰، ۱، ۲، ۳، ۴ و بینهایت باشد. برای دیدن حالتهای مختلف به تصاویر زیر نگاه کنید.
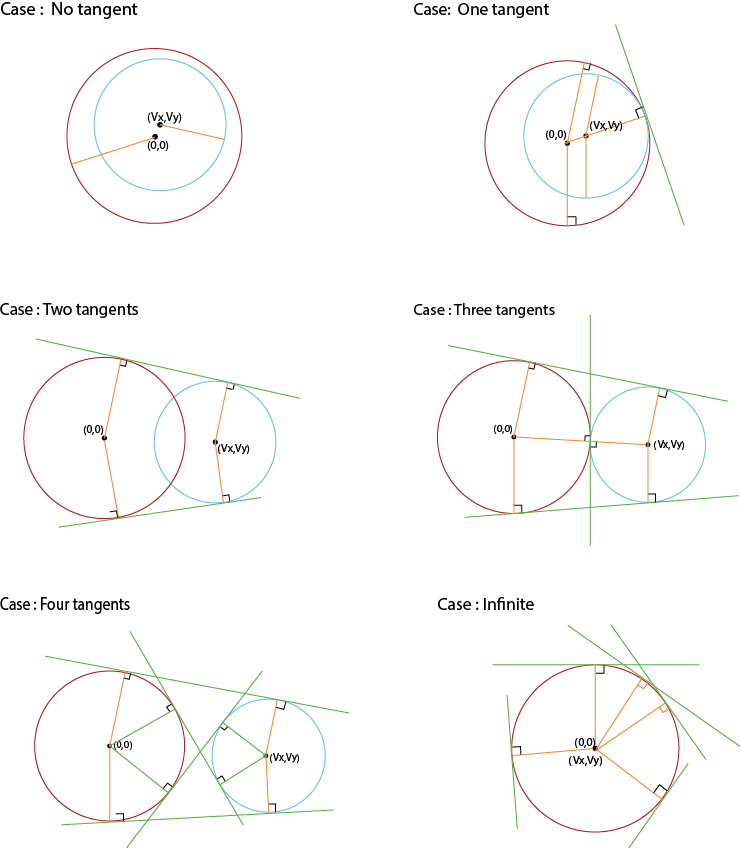
در اینجا، ما حالتهای تبهگن را در نظر نمیگیریم، یعنی زمانی که دایرهها بر هم منطبق هستند (در این حالت بینهایت مماس مشترک دارند)، یا یک دایره درون دیگری قرار دارد (در این حالت هیچ مماس مشترکی ندارند، یا اگر دایرهها مماس باشند، یک مماس مشترک وجود دارد).
در بیشتر موارد، دو دایره چهار مماس مشترک دارند.
اگر دایرهها مماس باشند، آنگاه سه مماس مشترک خواهند داشت، اما این را میتوان به عنوان یک حالت تبهگن در نظر گرفت: گویی دو مماس بر هم منطبق شدهاند.
علاوه بر این، الگوریتم توصیف شده در ادامه، در حالتی که یک یا هر دو دایره شعاع صفر داشته باشند نیز کار میکند: در این حالت به ترتیب دو یا یک مماس مشترک وجود خواهد داشت.
به طور خلاصه، ما همیشه به دنبال چهار مماس برای تمام حالات به جز حالت بینهایت مماس خواهیم بود (حالت بینهایت مماس باید به طور جداگانه بررسی شود و در اینجا مورد بحث قرار نمیگیرد). در حالتهای تبهگن، برخی از مماسها بر هم منطبق خواهند شد، اما با این وجود، این حالتها نیز در چارچوب کلی قرار میگیرند.
الگوریتم¶
برای سادگی الگوریتم، بدون از دست دادن کلیت مسئله، فرض میکنیم که مرکز دایره اول مختصات $(0, 0)$ را دارد. (اگر اینطور نباشد، میتوان با انتقال کل تصویر به این حالت رسید و پس از یافتن راه حل، خطوط به دست آمده را به جای اول خود بازگرداند).
$r_1$ و $r_2$ را شعاعهای دایره اول و دوم، و $(v_x, v_y)$ را مختصات مرکز دایره دوم و نقطه $v$ متفاوت از مبدأ در نظر میگیریم. (توجه: حالتی که هر دو دایره یکسان باشند را در نظر نمیگیریم).
برای حل مسئله، رویکردی کاملاً جبری در پیش میگیریم. ما باید تمام خطوط به شکل $ax + by + c = 0$ را پیدا کنیم که از مبدأ مختصات به فاصله $r_1$ و از نقطه $v$ به فاصله $r_2$ قرار دارند. علاوه بر این، شرط نرمالسازی خط راست را اعمال میکنیم: مجموع مربعات ضرایب $a$ و $b$ باید برابر با یک باشد (این کار ضروری است، در غیر این صورت، یک خط راست با بینهایت نمایش به شکل $ax + by + c = 0$ مطابقت خواهد داشت). در مجموع، به چنین دستگاه معادلاتی برای $a, b, c$ مورد نظر میرسیم:
برای خلاص شدن از قدر مطلق، توجه داشته باشید که تنها چهار راه برای باز کردن قدر مطلقها در این دستگاه وجود دارد. اگر باز کردن قدر مطلق را به این صورت درک کنیم که ضریب سمت راست ممکن است در -1 ضرب شود، میتوان تمام این روشها را با یک حالت کلی در نظر گرفت. به عبارت دیگر، به این دستگاه میرسیم:
با وارد کردن نمادگذاری $d_1 = \pm r_1$ و $d_2 = \pm r_2$، به این نتیجه میرسیم که دستگاه باید چهار راه حل داشته باشد:
حل این دستگاه به حل یک معادله درجه دو کاهش مییابد. ما از تمام محاسبات دست و پا گیر صرف نظر میکنیم و فوراً پاسخ آماده را ارائه میدهیم:
در مجموع به جای چهار جواب، هشت جواب به دست آوردیم. با این حال، به راحتی میتوان فهمید که جوابهای اضافی از کجا ناشی میشوند: در واقع، در دستگاه آخر، کافی است فقط یک جواب را در نظر بگیریم (مثلاً اولی را). در حقیقت، معنای هندسی در نظر گرفتن $\pm r_1$ و $\pm r_2$ روشن است: ما در واقع در حال بررسی این هستیم که خط در کدام سمت هر دایره قرار دارد. بنابراین، دو روشی که هنگام حل دستگاه آخر به وجود میآیند، زائد هستند: کافی است یکی از دو جواب را انتخاب کنیم (البته، در هر چهار حالت، باید همان خانواده از جوابها را انتخاب کنید).
آخرین چیزی که هنوز در نظر نگرفتهایم این است که در حالتی که دایره اول در ابتدا در مبدأ قرار نداشت، چگونه خطوط راست را انتقال دهیم. با این حال، همه چیز در اینجا ساده است: از خطی بودن معادله یک خط راست نتیجه میشود که مقدار $a \cdot x_0 + b \cdot y_0$ (که در آن $x_0$ و $y_0$ مختصات مرکز اصلی دایره اول هستند) باید از ضریب $c$ کم شود.
پیادهسازی¶
ابتدا تمام ساختارهای داده ضروری و سایر تعاریف کمکی را توصیف میکنیم:
struct pt {
double x, y;
pt operator- (pt p) {
pt res = { x-p.x, y-p.y };
return res;
}
};
struct circle : pt {
double r;
};
struct line {
double a, b, c;
};
const double EPS = 1E-9;
double sqr (double a) {
return a * a;
}
void tangents (pt c, double r1, double r2, vector<line> & ans) {
double r = r2 - r1;
double z = sqr(c.x) + sqr(c.y);
double d = z - sqr(r);
if (d < -EPS) return;
d = sqrt (abs (d));
line l;
l.a = (c.x * r + c.y * d) / z;
l.b = (c.y * r - c.x * d) / z;
l.c = r1;
ans.push_back (l);
}
vector<line> tangents (circle a, circle b) {
vector<line> ans;
for (int i=-1; i<=1; i+=2)
for (int j=-1; j<=1; j+=2)
tangents (b-a, a.r*i, b.r*j, ans);
for (size_t i=0; i<ans.size(); ++i)
ans[i].c -= ans[i].a * a.x + ans[i].b * a.y;
return ans;
}