جریان بیشینه - فورد-فالکرسون و ادموندز-کارپ¶
الگوریتم ادموندز-کارپ یک پیادهسازی از روش فورد-فالکرسون برای محاسبهی جریان بیشینه در یک شبکهی جریان است.
شبکهی جریان¶
ابتدا بیایید تعریف کنیم که شبکهی جریان (flow network)، جریان (flow) و جریان بیشینه (maximum flow) چه هستند.
یک شبکه (network) یک گراف جهتدار $G$ با رأسهای $V$ و یالهای $E$ است که همراه با یک تابع $c$ تعریف میشود. این تابع به هر یال $e \in E$ یک مقدار صحیح غیرمنفی به نام ظرفیت (capacity) آن یال نسبت میدهد. چنین شبکهای را یک شبکهی جریان (flow network) مینامیم، اگر علاوه بر این، دو رأس را برچسبگذاری کنیم: یکی به عنوان چشمه (source) و دیگری به عنوان چاهک (sink).
یک جریان (flow) در یک شبکهی جریان، تابعی به نام $f$ است که به هر یال $e$ یک مقدار صحیح غیرمنفی، یعنی همان جریان، نسبت میدهد. این تابع باید دو شرط زیر را برآورده کند:
جریان یک یال نمیتواند از ظرفیت آن تجاوز کند.
و مجموع جریان ورودی به یک رأس $u$ باید با مجموع جریان خروجی از آن رأس برابر باشد، مگر در رأسهای چشمه و چاهک.
رأس چشمه $s$ فقط جریان خروجی دارد و رأس چاهک $t$ فقط جریان ورودی دارد.
به راحتی میتوان دید که معادلهی زیر برقرار است:
یک تشبیه خوب برای شبکهی جریان، تصویرسازی زیر است: ما یالها را به عنوان لولههای آب در نظر میگیریم، ظرفیت یک یال حداکثر مقدار آبی است که میتواند در هر ثانیه از لوله عبور کند و جریان یک یال مقدار آبی است که در حال حاضر در هر ثانیه از لوله عبور میکند. این تشبیه، شرط اول جریان را توجیه میکند. آب بیشتری از ظرفیت یک لوله نمیتواند از آن عبور کند. رأسها مانند اتصالات عمل میکنند که آب از برخی لولهها به آنها وارد شده و سپس این رأسها آب را به نوعی بین لولههای دیگر توزیع میکنند. این موضوع نیز شرط دوم جریان را توجیه میکند. تمام آب ورودی به یک اتصال باید بین لولههای دیگر توزیع شود. آب نمیتواند به طور جادویی ناپدید یا ظاهر شود. چشمه $s$ منشأ تمام آب است و آب فقط میتواند در چاهک $t$ تخلیه شود.
تصویر زیر یک شبکهی جریان را نشان میدهد. مقدار اول روی هر یال نشاندهندهی جریان است که در ابتدا 0 است و مقدار دوم نشاندهندهی ظرفیت است.
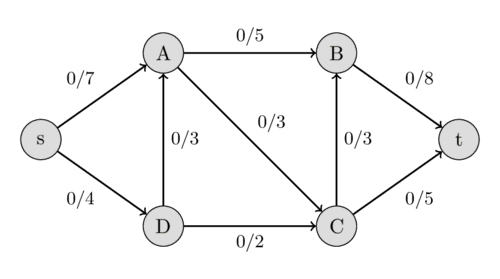
مقدار جریان یک شبکه برابر است با مجموع تمام جریانهایی که در چشمه $s$ تولید میشوند، یا معادل آن، مجموع تمام جریانهایی که توسط چاهک $t$ مصرف میشوند. یک جریان بیشینه (maximal flow) جریانی با بیشترین مقدار ممکن است. یافتن این جریان بیشینه در یک شبکهی جریان، مسئلهای است که میخواهیم حل کنیم.
در تصویرسازی با لولههای آب، مسئله را میتوان به این صورت فرموله کرد: چه مقدار آب میتوانیم از چشمه به چاهک از طریق لولهها منتقل کنیم؟
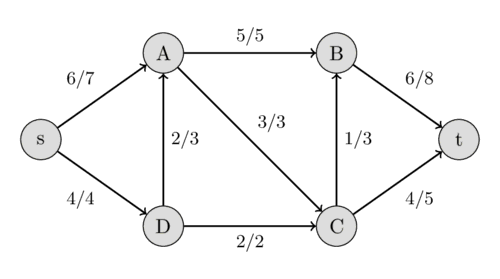
تصویر زیر جریان بیشینه را در این شبکهی جریان نشان میدهد.
روش فورد-فالکرسون¶
بیایید یک چیز دیگر را تعریف کنیم. ظرفیت باقیمانده (residual capacity) یک یال جهتدار برابر است با ظرفیت منهای جریان. باید توجه داشت که اگر جریانی در امتداد یک یال جهتدار $(u, v)$ وجود داشته باشد، آنگاه یال معکوس آن ظرفیت 0 دارد و میتوانیم جریان آن را به صورت $f((v, u)) = -f((u, v))$ تعریف کنیم. این کار ظرفیت باقیمانده را برای تمام یالهای معکوس نیز تعریف میکند. ما میتوانیم از تمام این یالها یک شبکهی باقیمانده (residual network) بسازیم، که شبکهای با همان رأسها و یالها است، اما از ظرفیتهای باقیمانده به عنوان ظرفیت استفاده میکنیم.
روش فورد-فالکرسون به این صورت عمل میکند. ابتدا، جریان هر یال را صفر قرار میدهیم. سپس به دنبال یک مسیر افزایشی (augmenting path) از $s$ به $t$ میگردیم. یک مسیر افزایشی، یک مسیر ساده در گراف باقیمانده است که ظرفیت باقیمانده برای تمام یالهای موجود در آن مسیر مثبت است. اگر چنین مسیری پیدا شود، میتوانیم جریان را در امتداد این یالها افزایش دهیم. ما به جستجوی مسیرهای افزایشی و افزایش جریان ادامه میدهیم. هنگامی که دیگر مسیر افزایشی وجود نداشته باشد، جریان بیشینه است.
بیایید با جزئیات بیشتری مشخص کنیم که افزایش جریان در امتداد یک مسیر افزایشی به چه معناست. فرض کنید $C$ کوچکترین ظرفیت باقیمانده در بین یالهای مسیر باشد. سپس جریان را به صورت زیر افزایش میدهیم: برای هر یال $(u, v)$ در مسیر، مقادیر $f((u, v)) ~\text{+=}~ C$ و $f((v, u)) ~\text{-=}~ C$ را بهروزرسانی میکنیم.
در اینجا مثالی برای نمایش این روش آورده شده است. از همان شبکهی جریان بالا استفاده میکنیم. در ابتدا با جریان 0 شروع میکنیم.

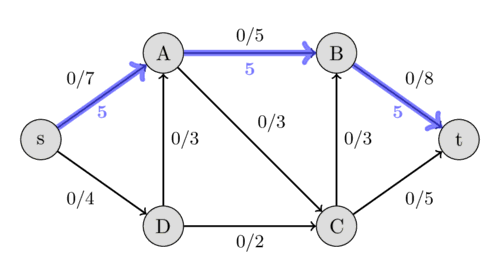
میتوانیم مسیر $s - A - B - t$ را با ظرفیتهای باقیماندهی 7، 5 و 8 پیدا کنیم. کمینهی آنها 5 است، بنابراین میتوانیم جریان را در امتداد این مسیر به اندازهی 5 افزایش دهیم. این کار جریانی به مقدار 5 برای شبکه ایجاد میکند.
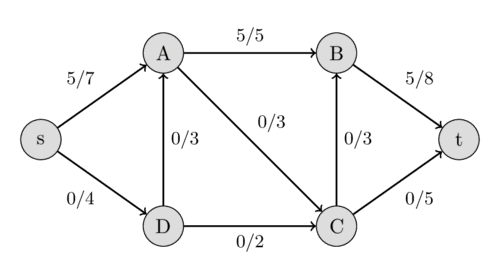
دوباره به دنبال یک مسیر افزایشی میگردیم، این بار مسیر $s - D - A - C - t$ را با ظرفیتهای باقیماندهی 4، 3، 3 و 5 پیدا میکنیم. بنابراین میتوانیم جریان را به اندازهی 3 افزایش دهیم و به جریان 8 برای شبکه میرسیم.
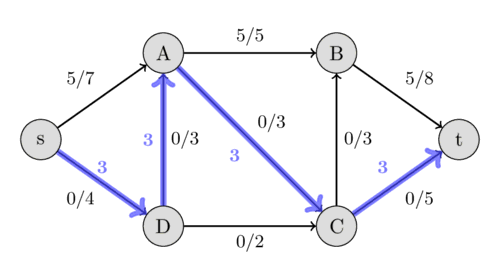
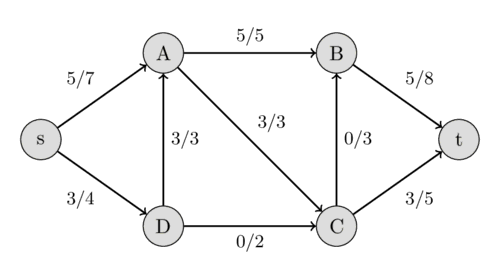
این بار مسیر $s - D - C - B - t$ را با ظرفیتهای باقیماندهی 1، 2، 3 و 3 پیدا میکنیم و در نتیجه، جریان را به اندازهی 1 افزایش میدهیم.
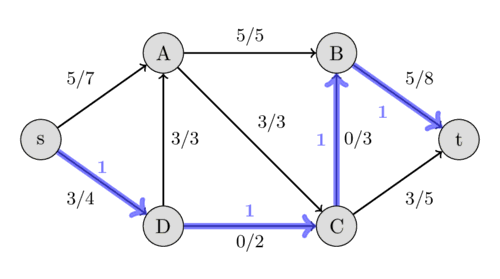
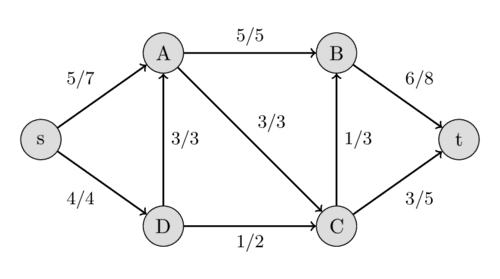
این بار مسیر افزایشی $s - A - D - C - t$ را با ظرفیتهای باقیماندهی 2، 3، 1 و 2 پیدا میکنیم. میتوانیم جریان را به اندازهی 1 افزایش دهیم. اما این مسیر بسیار جالب است. این مسیر شامل یال معکوس $(A, D)$ است. در شبکهی جریان اصلی، ما مجاز به ارسال هیچ جریانی از $A$ به $D$ نیستیم. اما چون از قبل جریانی به مقدار 3 از $D$ به $A$ داریم، این کار ممکن است. شهود پشت این قضیه به این صورت است: به جای ارسال جریان 3 از $D$ به $A$، ما فقط 2 واحد ارسال میکنیم و این کاهش را با ارسال یک جریان اضافی به مقدار 1 از $s$ به $A$ جبران میکنیم، که به ما اجازه میدهد یک جریان اضافی به مقدار 1 را در امتداد مسیر $D - C - t$ ارسال کنیم.
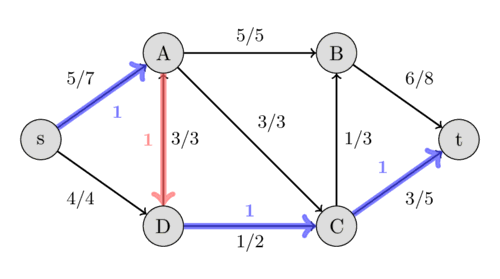

اکنون، پیدا کردن یک مسیر افزایشی بین $s$ و $t$ غیرممکن است، بنابراین این جریان به مقدار $10$ بیشینهی ممکن است. ما جریان بیشینه را پیدا کردهایم.
باید توجه داشت که روش فورد-فالکرسون روشی برای پیدا کردن مسیر افزایشی مشخص نمیکند. رویکردهای ممکن استفاده از DFS یا BFS هستند که هر دو در زمان $O(E)$ کار میکنند. اگر تمام ظرفیتهای شبکه اعداد صحیح باشند، آنگاه به ازای هر مسیر افزایشی، جریان شبکه حداقل 1 واحد افزایش مییابد (برای جزئیات بیشتر به قضیه جریان صحیح مراجعه کنید). بنابراین، پیچیدگی فورد-فالکرسون $O(E F)$ است که در آن $F$ جریان بیشینهی شبکه است. در مورد ظرفیتهای گویا، الگوریتم نیز به پایان میرسد، اما پیچیدگی آن کراندار نیست. در مورد ظرفیتهای گنگ، الگوریتم ممکن است هرگز به پایان نرسد و حتی ممکن است به جریان بیشینه همگرا نشود.
الگوریتم ادموندز-کارپ¶
الگوریتم ادموندز-کارپ صرفاً یک پیادهسازی از روش فورد-فالکرسون است که از BFS برای پیدا کردن مسیرهای افزایشی استفاده میکند. این الگوریتم برای اولین بار توسط یفیم دینیتز در سال 1970 منتشر شد و بعداً به طور مستقل توسط جک ادموندز و ریچارد کارپ در سال 1972 منتشر گردید.
پیچیدگی این الگوریتم را میتوان مستقل از جریان بیشینه بیان کرد. الگوریتم در زمان $O(V E^2)$ اجرا میشود، حتی برای ظرفیتهای گنگ. شهود این است که هر بار که یک مسیر افزایشی پیدا میکنیم، یکی از یالها اشباع میشود و فاصله از آن یال تا $s$ در صورتی که بعداً دوباره در یک مسیر افزایشی ظاهر شود، طولانیتر خواهد بود. طول مسیرهای ساده توسط $V$ کراندار است.
پیادهسازی¶
ماتریس capacity ظرفیت را برای هر جفت از رأسها ذخیره میکند.
adj لیست مجاورت گراف غیرجهتدار است، زیرا هنگام جستجوی مسیرهای افزایشی باید از یالهای معکوس یالهای جهتدار نیز استفاده کنیم.
تابع maxflow مقدار جریان بیشینه را برمیگرداند.
در طول اجرای الگوریتم، ماتریس capacity در واقع ظرفیت باقیماندهی شبکه را ذخیره میکند.
مقدار جریان در هر یال ذخیره نخواهد شد، اما به راحتی میتوان پیادهسازی را - با استفاده از یک ماتریس اضافی - گسترش داد تا جریان را نیز ذخیره و برگرداند.
int n;
vector<vector<int>> capacity;
vector<vector<int>> adj;
int bfs(int s, int t, vector<int>& parent) {
fill(parent.begin(), parent.end(), -1);
parent[s] = -2;
queue<pair<int, int>> q;
q.push({s, INF});
while (!q.empty()) {
int cur = q.front().first;
int flow = q.front().second;
q.pop();
for (int next : adj[cur]) {
if (parent[next] == -1 && capacity[cur][next]) {
parent[next] = cur;
int new_flow = min(flow, capacity[cur][next]);
if (next == t)
return new_flow;
q.push({next, new_flow});
}
}
}
return 0;
}
int maxflow(int s, int t) {
int flow = 0;
vector<int> parent(n);
int new_flow;
while (new_flow = bfs(s, t, parent)) {
flow += new_flow;
int cur = t;
while (cur != s) {
int prev = parent[cur];
capacity[prev][cur] -= new_flow;
capacity[cur][prev] += new_flow;
cur = prev;
}
}
return flow;
}
قضیه جریان صحیح¶
این قضیه بیان میکند که اگر تمام ظرفیتها در شبکه عدد صحیح باشند، آنگاه اندازهی جریان بیشینه یک عدد صحیح است و یک جریان بیشینه وجود دارد که در آن جریان هر یال نیز یک عدد صحیح است. به طور خاص، روش فورد-فالکرسون چنین جریانی را پیدا میکند.
قضیه جریان-بیشینه برش-کمینه¶
یک برش $s$-$t$ افرازی از رأسهای یک شبکهی جریان به دو مجموعه است، به طوری که یک مجموعه شامل چشمه $s$ و دیگری شامل چاهک $t$ باشد. ظرفیت یک برش $s$-$t$ به صورت مجموع ظرفیتهای یالهایی تعریف میشود که از سمت چشمه به سمت چاهک میروند.
بدیهی است که ما نمیتوانیم جریانی بیشتر از ظرفیت هر برش $s$-$t$ از $s$ به $t$ ارسال کنیم. بنابراین، جریان بیشینه توسط ظرفیت برش کمینه کراندار است.
قضیه جریان-بیشینه برش-کمینه حتی از این هم فراتر میرود. این قضیه بیان میکند که ظرفیت جریان بیشینه باید برابر با ظرفیت برش کمینه باشد.
در تصویر زیر، میتوانید برش کمینه را برای شبکهی جریانی که قبلاً استفاده کردیم، مشاهده کنید. این تصویر نشان میدهد که ظرفیت برش بین دو مجموعه $\{s, A, D\}$ و $\{B, C, t\}$ برابر با $5 + 3 + 2 = 10$ است که با جریان بیشینهای که پیدا کردیم برابر است. برشهای دیگر ظرفیت بیشتری خواهند داشت، مثلاً ظرفیت بین مجموعههای $\{s, A\}$ و $\{B, C, D, t\}$ برابر $4 + 3 + 5 = 12$ است.
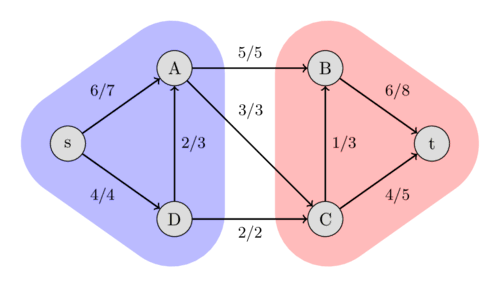
یک برش کمینه را میتوان پس از محاسبهی جریان بیشینه با استفاده از روش فورد-فالکرسون پیدا کرد. یک برش کمینه ممکن به شرح زیر است: مجموعهی تمام رأسهایی که از $s$ در گراف باقیمانده قابل دسترسی هستند (با استفاده از یالهایی با ظرفیت باقیمانده مثبت)، و مجموعهی تمام رأسهای دیگر. این افراز را میتوان به راحتی با استفاده از DFS که از $s$ شروع میشود، پیدا کرد.