پایینترین جد مشترک - $O(\sqrt{N})$ و $O(\log N)$ با پیشپردازش $O(N)$¶
درخت $G$ داده شده است. با توجه به پرسشهایی به شکل $(v_1, v_2)$، برای هر پرسش باید پایینترین جد مشترک (least common ancestor یا LCA) را پیدا کنید، یعنی رأسی مانند $v$ که هم روی مسیر از ریشه به $v_1$ و هم روی مسیر از ریشه به $v_2$ قرار دارد و در پایینترین سطح ممکن است. به عبارت دیگر، رأس $v$ مورد نظر، عمیقترین (پایینترین) جد مشترک دو رأس $v_1$ و $v_2$ است. واضح است که پایینترین جد مشترک آنها روی کوتاهترین مسیر بین $v_1$ و $v_2$ قرار دارد. همچنین، اگر $v_1$ جد $v_2$ باشد، آنگاه $v_1$ پایینترین جد مشترک آنها است.
ایده الگوریتم¶
قبل از پاسخ به پرسشها، باید درخت را پیشپردازش کنیم. یک پیمایش DFS را از ریشه شروع میکنیم و یک لیست به نام $\text{euler}$ میسازیم که ترتیب رأسهایی را که بازدید میکنیم ذخیره میکند (یک رأس هنگام اولین بازدید و پس از بازگشت پیمایش DFS از فرزندانش به لیست اضافه میشود). این پیمایش به تور اویلری درخت نیز معروف است. واضح است که اندازه این لیست $O(N)$ خواهد بود. همچنین باید آرایهی $\text{first}[0..N-1]$ را بسازیم که برای هر رأس $i$، اولین وقوع آن را در لیست $\text{euler}$ ذخیره کند. یعنی، اولین موقعیت در $\text{euler}$ که شرط $\text{euler}[\text{first}[i]] = i$ برقرار باشد. همچنین با استفاده از DFS میتوانیم ارتفاع هر گره (فاصله از ریشه) را پیدا کرده و آن را در آرایهی $\text{height}[0..N-1]$ ذخیره کنیم.
حال چگونه میتوانیم با استفاده از تور اویلری و دو آرایه کمکی به پرسشها پاسخ دهیم؟ فرض کنید پرسش یک زوج $(v_1, v_2)$ باشد. رأسهایی را که در تور اویلری بین اولین بازدید از $v_1$ و اولین بازدید از $v_2$ مشاهده میکنیم در نظر بگیرید. به راحتی میتوان دید که $\text{LCA}(v_1, v_2)$ رأسی با کمترین ارتفاع در این بخش از مسیر است. قبلاً اشاره کردیم که LCA باید بخشی از کوتاهترین مسیر بین $v_1$ و $v_2$ باشد. واضح است که باید رأسی با کمترین ارتفاع نیز باشد. در تور اویلری، ما اساساً کوتاهترین مسیر را طی میکنیم، با این تفاوت که تمام زیردرختهایی را که در مسیر با آنها مواجه میشویم نیز بازدید میکنیم. اما تمام رأسهای موجود در این زیردرختها در سطحی پایینتر از LCA قرار دارند و در نتیجه ارتفاع بیشتری دارند. بنابراین، $\text{LCA}(v_1, v_2)$ را میتوان به طور یکتا با پیدا کردن رأسی با کمترین ارتفاع در تور اویلری بین $\text{first}(v_1)$ و $\text{first}(v_2)$ تعیین کرد.
بیایید این ایده را با یک مثال توضیح دهیم. گراف زیر و تور اویلری آن را به همراه ارتفاعهای متناظر در نظر بگیرید:
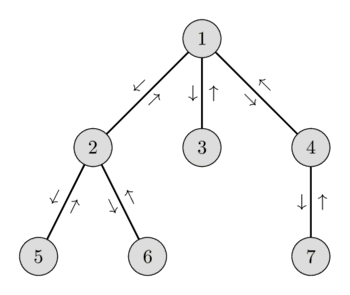
در پیمایش بین اولین بازدید از رأس ۶ و اولین بازدید از رأس ۴، ما از رأسهای $[6, 2, 1, 3, 1, 4]$ عبور میکنیم. در میان این رأسها، رأس ۱ کمترین ارتفاع را دارد، بنابراین $\text{LCA(6, 4) = 1}$ است.
به طور خلاصه: برای پاسخ به یک پرسش، فقط باید رأس با کمترین ارتفاع را در آرایه $\text{euler}$ در بازه $\text{first}[v_1]$ تا $\text{first}[v_2]$ پیدا کنیم. بنابراین، مسئله LCA به مسئله RMQ (یافتن کمینه در یک بازه) تبدیل میشود.
با استفاده از تجزیه ریشه دوم (Sqrt-Decomposition)، میتوان به راه حلی دست یافت که هر پرسش را در زمان $O(\sqrt{N})$ با پیشپردازش $O(N)$ پاسخ میدهد.
با استفاده از درخت بازهها (Segment Tree) میتوانید هر پرسش را در زمان $O(\log N)$ با پیشپردازش $O(N)$ پاسخ دهید.
از آنجا که تقریباً هیچگاه مقادیر ذخیرهشده بهروزرسانی نمیشوند، استفاده از جدول پراکنده (Sparse Table) میتواند انتخاب بهتری باشد که پاسخدهی به پرسشها را در زمان $O(1)$ با زمان ساخت $O(N\log N)$ ممکن میسازد.
پیادهسازی¶
در پیادهسازی زیر برای الگوریتم LCA از درخت بازهها استفاده شده است.
struct LCA {
vector<int> height, euler, first, segtree;
vector<bool> visited;
int n;
LCA(vector<vector<int>> &adj, int root = 0) {
n = adj.size();
height.resize(n);
first.resize(n);
euler.reserve(n * 2);
visited.assign(n, false);
dfs(adj, root);
int m = euler.size();
segtree.resize(m * 4);
build(1, 0, m - 1);
}
void dfs(vector<vector<int>> &adj, int node, int h = 0) {
visited[node] = true;
height[node] = h;
first[node] = euler.size();
euler.push_back(node);
for (auto to : adj[node]) {
if (!visited[to]) {
dfs(adj, to, h + 1);
euler.push_back(node);
}
}
}
void build(int node, int b, int e) {
if (b == e) {
segtree[node] = euler[b];
} else {
int mid = (b + e) / 2;
build(node << 1, b, mid);
build(node << 1 | 1, mid + 1, e);
int l = segtree[node << 1], r = segtree[node << 1 | 1];
segtree[node] = (height[l] < height[r]) ? l : r;
}
}
int query(int node, int b, int e, int L, int R) {
if (b > R || e < L)
return -1;
if (b >= L && e <= R)
return segtree[node];
int mid = (b + e) >> 1;
int left = query(node << 1, b, mid, L, R);
int right = query(node << 1 | 1, mid + 1, e, L, R);
if (left == -1) return right;
if (right == -1) return left;
return height[left] < height[right] ? left : right;
}
int lca(int u, int v) {
int left = first[u], right = first[v];
if (left > right)
swap(left, right);
return query(1, 0, euler.size() - 1, left, right);
}
};
مسائل تمرینی¶
- SPOJ: LCA
- SPOJ: DISQUERY
- TIMUS: 1471. Distance in the Tree
- CODEFORCES: Design Tutorial: Inverse the Problem
- CODECHEF: Lowest Common Ancestor
- SPOJ - Lowest Common Ancestor
- SPOJ - Ada and Orange Tree
- DevSkill - Motoku (archived)
- UVA 12655 - Trucks
- Codechef - Pishty and Tree
- UVA - 12533 - Joining Couples
- Codechef - So close yet So Far
- Codeforces - Drivers Dissatisfaction
- UVA 11354 - Bond
- SPOJ - Querry on a tree II
- Codeforces - Best Edge Weight
- Codeforces - Misha, Grisha and Underground
- SPOJ - Nlogonian Tickets
- Codeforces - Rowena Rawenclaws Diadem