تجزیه عمودی (Vertical decomposition)¶
نمای کلی¶
تجزیه عمودی (Vertical decomposition) یک تکنیک قدرتمند است که در مسائل مختلف هندسه استفاده میشود. ایده کلی این است که صفحه را به چندین نوار عمودی با برخی ویژگیهای «خوب» تقسیم کنیم و مسئله را برای هر یک از این نوارها به طور مستقل حل کنیم. این ایده را با چند مثال توضیح خواهیم داد.
مساحت اجتماع مثلثها¶
فرض کنید $n$ مثلث در یک صفحه وجود دارد و میخواهیم مساحت اجتماع آنها را پیدا کنیم. اگر مثلثها با هم تلاقی نداشتند، مسئله آسان بود. بنابراین، با رسم خطوط عمودی از تمام رأسها و تمام نقاط تلاقی اضلاع مثلثهای مختلف، صفحه را به نوارهای عمودی تقسیم میکنیم تا از این تلاقیها خلاص شویم. ممکن است $O(n^2)$ خط از این نوع وجود داشته باشد، بنابراین $O(n^2)$ نوار به دست میآوریم. حالا یک نوار عمودی را در نظر بگیرید. هر پارهخط غیرعمودی یا این نوار را از چپ به راست قطع میکند یا اصلاً آن را قطع نمیکند. همچنین، هیچ دو پارهخطی دقیقاً داخل نوار یکدیگر را قطع نمیکنند. این بدان معناست که بخشی از اجتماع مثلثها که درون این نوار قرار دارد، از ذوزنقههای مجزا تشکیل شده است که پایههای آنها روی اضلاع نوار قرار دارند. این ویژگی به ما اجازه میدهد تا مساحت داخل هر نوار را با یک الگوریتم خط جاروب (scanline) محاسبه کنیم. هر پارهخطی که نوار را قطع میکند، یا بالایی است یا پایینی، بسته به اینکه فضای داخلی مثلث مربوطه بالای پارهخط باشد یا پایین آن. میتوانیم هر پارهخط بالایی را به عنوان یک پرانتز باز و هر پارهخط پایینی را به عنوان یک پرانتز بسته در نظر بگیریم و با تجزیه توالی پرانتزها به توالیهای پرانتز صحیح کوچکتر، نوار را به ذوزنقه تجزیه کنیم. این الگوریتم به زمان $O(n^3\log n)$ و حافظه $O(n^2)$ نیاز دارد.
بهینهسازی ۱¶
ابتدا زمان اجرا را به $O(n^2\log n)$ کاهش میدهیم. به جای تولید ذوزنقه برای هر نوار، یک ضلع مثلث (پارهخط $s = (s_0, s_1)$) را ثابت میکنیم و مجموعهای از نوارها را پیدا میکنیم که در آنها این پارهخط ضلع یک ذوزنقه باشد. توجه داشته باشید که در این حالت، فقط باید نوارهایی را پیدا کنیم که در آنها تراز (balance) پرانتزهای زیر (یا بالای، در مورد پارهخط پایینی) $s$ صفر باشد. این بدان معناست که به جای اجرای خط جاروب عمودی برای هر نوار، میتوانیم یک خط جاروب افقی برای تمام بخشهای سایر پارهخطها که بر تراز پرانتزها نسبت به $s$ تأثیر میگذارند، اجرا کنیم. برای سادگی، نشان میدهیم که چگونه این کار را برای یک پارهخط بالایی انجام دهیم؛ الگوریتم برای پارهخطهای پایینی مشابه است. یک پارهخط غیرعمودی دیگر $t = (t_0, t_1)$ را در نظر بگیرید و اشتراک $[x_1, x_2]$ تصویرهای $s$ و $t$ بر روی محور $Ox$ را پیدا کنید. اگر این اشتراک خالی باشد یا از یک نقطه تشکیل شده باشد، میتوان $t$ را نادیده گرفت، زیرا $s$ و $t$ فضای داخلی یک نوار یکسان را قطع نمیکنند. در غیر این صورت، اشتراک $I$ بین $s$ و $t$ را در نظر بگیرید. سه حالت وجود دارد.
-
$I = \varnothing$
در این حالت، $t$ در بازه $[x_1, x_2]$ یا بالای $s$ قرار دارد یا پایین آن. اگر $t$ بالا باشد، تأثیری بر اینکه $s$ ضلع یک ذوزنقه باشد یا نه، ندارد. اگر $t$ پایین $s$ باشد، باید بسته به اینکه $t$ بالایی است یا پایینی، $1$ یا $-1$ را به تراز توالی پرانتزها برای تمام نوارهای موجود در $[x_1, x_2]$ اضافه کنیم.
-
$I$ از یک نقطه $p$ تشکیل شده است
این حالت را میتوان با تقسیم $[x_1, x_2]$ به $[x_1, p_x]$ و $[p_x, x_2]$ به حالت قبلی کاهش داد.
-
$I$ یک پارهخط $l$ است
این حالت به این معناست که بخشهایی از $s$ و $t$ برای $x\in[x_1, x_2]$ بر هم منطبق هستند. اگر $t$ پایینی باشد، واضح است که $s$ ضلع یک ذوزنقه نیست. در غیر این صورت، ممکن است هم $s$ و هم $t$ بتوانند به عنوان ضلع یک ذوزنقه در نظر گرفته شوند. برای حل این ابهام، میتوانیم تصمیم بگیریم که فقط پارهخطی که کمترین شاخص (index) را دارد به عنوان ضلع در نظر گرفته شود (اینجا فرض میکنیم که اضلاع مثلث به نحوی شمارهگذاری شدهاند). بنابراین، اگر $index(s) < index(t)$ باشد، باید این حالت را نادیده بگیریم؛ در غیر این صورت، باید علامتگذاری کنیم که $s$ هرگز نمیتواند در بازه $[x_1, x_2]$ یک ضلع باشد (مثلاً با اضافه کردن یک رویداد متناظر با تراز $-2$).
در اینجا یک نمایش گرافیکی از این سه حالت آورده شده است.
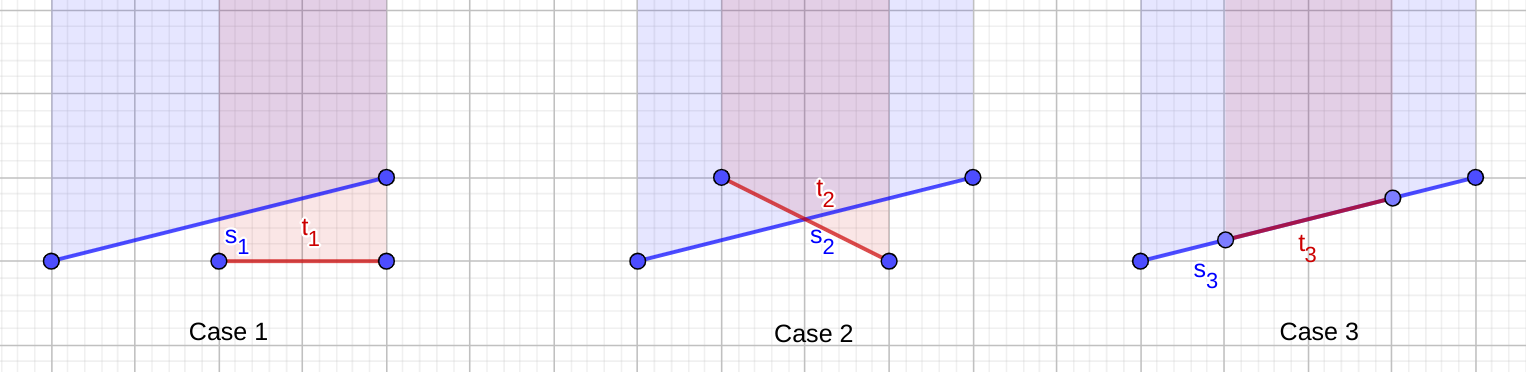
در نهایت، باید به پردازش تمام جمعهای $1$ یا $-1$ در تمام نوارهای موجود در $[x_1, x_2]$ اشاره کنیم. برای هر اضافه کردن $w$ در بازه $[x_1, x_2]$، میتوانیم رویدادهای $(x_1, w)$ و $(x_2, -w)$ را ایجاد کرده و همه این رویدادها را با یک خط جاروب (sweep line) پردازش کنیم.
بهینهسازی ۲¶
توجه داشته باشید که اگر بهینهسازی قبلی را اعمال کنیم، دیگر نیازی به پیدا کردن صریح همه نوارها نداریم. این کار مصرف حافظه را به $O(n)$ کاهش میدهد.
اشتراک چندضلعیهای محدب¶
کاربرد دیگر تجزیه عمودی، محاسبه اشتراک دو چندضلعی محدب در زمان خطی است. فرض کنید صفحه توسط خطوط عمودی که از هر رأس هر چندضلعی عبور میکنند، به نوارهای عمودی تقسیم شده است. سپس اگر یکی از چندضلعیهای ورودی و یک نوار را در نظر بگیریم، اشتراک آنها یا یک ذوزنقه، یک مثلث یا یک نقطه است. بنابراین، میتوانیم به سادگی این اشکال را برای هر نوار عمودی با هم تلاقی دهیم و این اشتراکها را در یک چندضلعی واحد ادغام کنیم.
پیادهسازی¶
در زیر کدی آمده است که مساحت اجتماع مجموعهای از مثلثها را در زمان $O(n^2\log n)$ و با حافظه $O(n)$ محاسبه میکند.
typedef double dbl;
const dbl eps = 1e-9;
inline bool eq(dbl x, dbl y){
return fabs(x - y) < eps;
}
inline bool lt(dbl x, dbl y){
return x < y - eps;
}
inline bool gt(dbl x, dbl y){
return x > y + eps;
}
inline bool le(dbl x, dbl y){
return x < y + eps;
}
inline bool ge(dbl x, dbl y){
return x > y - eps;
}
struct pt{
dbl x, y;
inline pt operator - (const pt & p)const{
return pt{x - p.x, y - p.y};
}
inline pt operator + (const pt & p)const{
return pt{x + p.x, y + p.y};
}
inline pt operator * (dbl a)const{
return pt{x * a, y * a};
}
inline dbl cross(const pt & p)const{
return x * p.y - y * p.x;
}
inline dbl dot(const pt & p)const{
return x * p.x + y * p.y;
}
inline bool operator == (const pt & p)const{
return eq(x, p.x) && eq(y, p.y);
}
};
struct Line{
pt p[2];
Line(){}
Line(pt a, pt b):p{a, b}{}
pt vec()const{
return p[1] - p[0];
}
pt& operator [](size_t i){
return p[i];
}
};
inline bool lexComp(const pt & l, const pt & r){
if(fabs(l.x - r.x) > eps){
return l.x < r.x;
}
else return l.y < r.y;
}
vector<pt> interSegSeg(Line l1, Line l2){
if(eq(l1.vec().cross(l2.vec()), 0)){
if(!eq(l1.vec().cross(l2[0] - l1[0]), 0))
return {};
if(!lexComp(l1[0], l1[1]))
swap(l1[0], l1[1]);
if(!lexComp(l2[0], l2[1]))
swap(l2[0], l2[1]);
pt l = lexComp(l1[0], l2[0]) ? l2[0] : l1[0];
pt r = lexComp(l1[1], l2[1]) ? l1[1] : l2[1];
if(l == r)
return {l};
else return lexComp(l, r) ? vector<pt>{l, r} : vector<pt>();
}
else{
dbl s = (l2[0] - l1[0]).cross(l2.vec()) / l1.vec().cross(l2.vec());
pt inter = l1[0] + l1.vec() * s;
if(ge(s, 0) && le(s, 1) && le((l2[0] - inter).dot(l2[1] - inter), 0))
return {inter};
else
return {};
}
}
inline char get_segtype(Line segment, pt other_point){
if(eq(segment[0].x, segment[1].x))
return 0;
if(!lexComp(segment[0], segment[1]))
swap(segment[0], segment[1]);
return (segment[1] - segment[0]).cross(other_point - segment[0]) > 0 ? 1 : -1;
}
dbl union_area(vector<tuple<pt, pt, pt> > triangles){
vector<Line> segments(3 * triangles.size());
vector<char> segtype(segments.size());
for(size_t i = 0; i < triangles.size(); i++){
pt a, b, c;
tie(a, b, c) = triangles[i];
segments[3 * i] = lexComp(a, b) ? Line(a, b) : Line(b, a);
segtype[3 * i] = get_segtype(segments[3 * i], c);
segments[3 * i + 1] = lexComp(b, c) ? Line(b, c) : Line(c, b);
segtype[3 * i + 1] = get_segtype(segments[3 * i + 1], a);
segments[3 * i + 2] = lexComp(c, a) ? Line(c, a) : Line(a, c);
segtype[3 * i + 2] = get_segtype(segments[3 * i + 2], b);
}
vector<dbl> k(segments.size()), b(segments.size());
for(size_t i = 0; i < segments.size(); i++){
if(segtype[i]){
k[i] = (segments[i][1].y - segments[i][0].y) / (segments[i][1].x - segments[i][0].x);
b[i] = segments[i][0].y - k[i] * segments[i][0].x;
}
}
dbl ans = 0;
for(size_t i = 0; i < segments.size(); i++){
if(!segtype[i])
continue;
dbl l = segments[i][0].x, r = segments[i][1].x;
vector<pair<dbl, int> > evts;
for(size_t j = 0; j < segments.size(); j++){
if(!segtype[j] || i == j)
continue;
dbl l1 = segments[j][0].x, r1 = segments[j][1].x;
if(ge(l1, r) || ge(l, r1))
continue;
dbl common_l = max(l, l1), common_r = min(r, r1);
auto pts = interSegSeg(segments[i], segments[j]);
if(pts.empty()){
dbl yl1 = k[j] * common_l + b[j];
dbl yl = k[i] * common_l + b[i];
if(lt(yl1, yl) == (segtype[i] == 1)){
int evt_type = -segtype[i] * segtype[j];
evts.emplace_back(common_l, evt_type);
evts.emplace_back(common_r, -evt_type);
}
}
else if(pts.size() == 1u){
dbl yl = k[i] * common_l + b[i], yl1 = k[j] * common_l + b[j];
int evt_type = -segtype[i] * segtype[j];
if(lt(yl1, yl) == (segtype[i] == 1)){
evts.emplace_back(common_l, evt_type);
evts.emplace_back(pts[0].x, -evt_type);
}
yl = k[i] * common_r + b[i], yl1 = k[j] * common_r + b[j];
if(lt(yl1, yl) == (segtype[i] == 1)){
evts.emplace_back(pts[0].x, evt_type);
evts.emplace_back(common_r, -evt_type);
}
}
else{
if(segtype[j] != segtype[i] || j > i){
evts.emplace_back(common_l, -2);
evts.emplace_back(common_r, 2);
}
}
}
evts.emplace_back(l, 0);
sort(evts.begin(), evts.end());
size_t j = 0;
int balance = 0;
while(j < evts.size()){
size_t ptr = j;
while(ptr < evts.size() && eq(evts[j].first, evts[ptr].first)){
balance += evts[ptr].second;
++ptr;
}
if(!balance && !eq(evts[j].first, r)){
dbl next_x = ptr == evts.size() ? r : evts[ptr].first;
ans -= segtype[i] * (k[i] * (next_x + evts[j].first) + 2 * b[i]) * (next_x - evts[j].first);
}
j = ptr;
}
}
return ans/2;
}