تجزیهٔ اعداد صحیح¶
در این مقاله چندین الگوریتم برای تجزیهٔ اعداد صحیح را لیست میکنیم که هر کدام بسته به ورودیشان میتوانند سریع یا با درجات متفاوتی از کندی عمل کنند.
توجه کنید، اگر عددی که میخواهید تجزیه کنید در واقع یک عدد اول باشد، اکثر الگوریتمها بسیار کند اجرا میشوند. این موضوع به ویژه برای الگوریتمهای تجزیهٔ فرما، p-1 پولارد و rho پولارد صادق است. بنابراین، منطقیترین کار این است که قبل از تلاش برای تجزیهٔ عدد، یک آزمون اول بودن احتمالی (یا یک آزمون قطعی سریع) روی آن انجام دهید.
تقسیم آزمایشی¶
این ابتداییترین الگوریتم برای یافتن تجزیه به عوامل اول است.
ما عدد را بر هر مقسومعلیه ممکن $d$ تقسیم میکنیم. میتوان مشاهده کرد که غیرممکن است تمام عوامل اول یک عدد مرکب $n$ بزرگتر از $\sqrt{n}$ باشند. بنابراین، تنها کافی است مقسومعلیههای $2 \le d \le \sqrt{n}$ را آزمایش کنیم، که این کار تجزیه به عوامل اول را در زمان $O(\sqrt{n})$ به ما میدهد. (این زمان شبهچندجملهای است، یعنی بر حسب مقدار ورودی چندجملهای است اما بر حسب تعداد بیتهای ورودی نمایی است.)
کوچکترین مقسومعلیه باید یک عدد اول باشد. ما عامل پیدا شده را از عدد حذف کرده و فرآیند را ادامه میدهیم. اگر نتوانیم هیچ مقسومعلیهی در بازهٔ $[2; \sqrt{n}]$ پیدا کنیم، آنگاه خود عدد باید اول باشد.
vector<long long> trial_division1(long long n) {
vector<long long> factorization;
for (long long d = 2; d * d <= n; d++) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
تجزیه چرخ¶
این یک بهینهسازی برای روش تقسیم آزمایشی است. وقتی میدانیم که عدد بر 2 بخشپذیر نیست، دیگر نیازی به بررسی سایر اعداد زوج نداریم. این کار باعث میشود تنها $50\%$ از اعداد برای بررسی باقی بمانند. پس از حذف عامل 2 و رسیدن به یک عدد فرد، میتوانیم به سادگی با 3 شروع کرده و فقط اعداد فرد دیگر را بررسی کنیم.
vector<long long> trial_division2(long long n) {
vector<long long> factorization;
while (n % 2 == 0) {
factorization.push_back(2);
n /= 2;
}
for (long long d = 3; d * d <= n; d += 2) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
این روش را میتوان بیشتر گسترش داد. اگر عدد بر 3 بخشپذیر نباشد، میتوانیم تمام مضربهای دیگر 3 را نیز در محاسبات آینده نادیده بگیریم. بنابراین تنها کافی است اعداد $5, 7, 11, 13, 17, 19, 23, \dots$ را بررسی کنیم. میتوانیم یک الگو در این اعداد باقیمانده مشاهده کنیم. باید تمام اعدادی را بررسی کنیم که $d \bmod 6 = 1$ و $d \bmod 6 = 5$ باشند. بنابراین این کار باعث میشود تنها $33.3\%$ درصد از اعداد برای بررسی باقی بمانند. میتوانیم این را با حذف عوامل اول 2 و 3 در ابتدا پیادهسازی کنیم و پس از آن با 5 شروع کرده و فقط باقیماندههای $1$ و $5$ به پیمانهٔ $6$ را بشماریم.
در اینجا یک پیادهسازی برای اعداد اول 2، 3 و 5 آمده است. راحتتر است که گامهای پرش را در یک آرایه ذخیره کنیم.
vector<long long> trial_division3(long long n) {
vector<long long> factorization;
for (int d : {2, 3, 5}) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
static array<int, 8> increments = {4, 2, 4, 2, 4, 6, 2, 6};
int i = 0;
for (long long d = 7; d * d <= n; d += increments[i++]) {
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
if (i == 8)
i = 0;
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
اگر به گسترش این روش برای در بر گرفتن اعداد اول بیشتر ادامه دهیم، میتوان به درصدهای بهتری دست یافت، اما لیستهای پرش بزرگتر خواهند شد.
اعداد اول از پیش محاسبهشده¶
با گسترش نامحدود روش تجزیه چرخ، در نهایت تنها اعداد اول برای بررسی باقی میمانند. یک راه خوب برای این کار، پیشمحاسبهٔ تمام اعداد اول تا $\sqrt{n}$ با استفاده از غربال اراتوستن و سپس آزمودن تکتک آنها است.
vector<long long> primes;
vector<long long> trial_division4(long long n) {
vector<long long> factorization;
for (long long d : primes) {
if (d * d > n)
break;
while (n % d == 0) {
factorization.push_back(d);
n /= d;
}
}
if (n > 1)
factorization.push_back(n);
return factorization;
}
روش تجزیه فرما¶
میتوانیم یک عدد مرکب فرد $n = p \cdot q$ را به صورت تفاضل دو مربع $n = a^2 - b^2$ بنویسیم:
روش تجزیه فرما سعی میکند از این واقعیت با حدس زدن مربع اول، $a^2$، و بررسی اینکه آیا بخش باقیمانده، $b^2 = a^2 - n$، نیز یک عدد مربع کامل است، بهرهبرداری کند. اگر چنین باشد، آنگاه عوامل $a - b$ و $a + b$ از $n$ را پیدا کردهایم.
int fermat(int n) {
int a = ceil(sqrt(n));
int b2 = a*a - n;
int b = round(sqrt(b2));
while (b * b != b2) {
a = a + 1;
b2 = a*a - n;
b = round(sqrt(b2));
}
return a - b;
}
این روش تجزیه میتواند بسیار سریع باشد اگر اختلاف بین دو عامل $p$ و $q$ کم باشد. الگوریتم در زمان $O(|p - q|)$ اجرا میشود. با این حال در عمل، این روش به ندرت استفاده میشود. هنگامی که عوامل از هم دورتر میشوند، این روش بسیار کند عمل میکند.
با این وجود، هنوز تعداد زیادی گزینه بهینهسازی برای این رویکرد وجود دارد. با نگاه کردن به مربعهای $a^2$ به پیمانه یک عدد کوچک ثابت، میتوان مشاهده کرد که نیازی به بررسی برخی مقادیر $a$ نیست، زیرا آنها نمیتوانند یک عدد مربع کامل $a^2 - n$ تولید کنند.
روش $p - 1$ پولارد¶
بسیار محتمل است که یک عدد $n$ حداقل یک عامل اول $p$ داشته باشد به طوری که $p - 1$ برای یک $\mathrm{B}$ کوچک، $\mathrm{B}$-powersmooth باشد. یک عدد صحیح $m$ را $\mathrm{B}$-powersmooth میگویند اگر هر توان اولی که $m$ را عاد میکند، حداکثر برابر با $\mathrm{B}$ باشد. به طور رسمی، فرض کنید $\mathrm{B} \geqslant 1$ و $m$ هر عدد صحیح مثبتی باشد. فرض کنید تجزیه به عوامل اول $m$ به صورت $m = \prod {q_i}^{e_i}$ باشد که در آن هر $q_i$ یک عدد اول و $e_i \geqslant 1$ است. آنگاه $m$ را $\mathrm{B}$-powersmooth میگوییم اگر برای تمام $i$ ها داشته باشیم ${q_i}^{e_i} \leqslant \mathrm{B}$. برای مثال، تجزیه به عوامل اول عدد $4817191$ برابر با $1303 \cdot 3697$ است. و مقادیر $1303 - 1$ و $3697 - 1$ به ترتیب $31$-powersmooth و $16$-powersmooth هستند، زیرا $1303 - 1 = 2 \cdot 3 \cdot 7 \cdot 31$ و $3697 - 1 = 2^4 \cdot 3 \cdot 7 \cdot 11$. در سال 1974 جان پولارد روشی را برای استخراج عوامل $p$ از یک عدد مرکب ابداع کرد، به طوری که $p-1$ یک عدد $\mathrm{B}$-powersmooth باشد.
ایدهٔ این روش از قضیه کوچک فرما میآید. فرض کنید تجزیهٔ $n$ به صورت $n = p \cdot q$ باشد. قضیه میگوید اگر $a$ نسبت به $p$ اول باشد، گزارهٔ زیر برقرار است:
این همچنین به این معناست که
بنابراین برای هر $M$ که $p - 1 | M$، میدانیم که $a^M \equiv 1 \pmod{p}$ است. این یعنی $a^M - 1 = p \cdot r$ و به همین دلیل $p | \gcd(a^M - 1, n)$ نیز برقرار است.
بنابراین، اگر برای عاملی مانند $p$ از $n$، داشته باشیم که $p-1$ عدد $M$ را عاد کند، میتوانیم با استفاده از الگوریتم اقلیدس یک عامل را استخراج کنیم.
واضح است که کوچکترین $M$ که مضربی از هر عدد $\mathrm{B}$-powersmooth باشد، برابر است با $\text{lcm}(1,~2~,3~,4~,~\dots,~B)$. یا به طور جایگزین:
توجه کنید، اگر $p-1$ برای تمام عوامل اول $p$ از $n$ عدد $M$ را عاد کند، آنگاه $\gcd(a^M - 1, n)$ برابر با خود $n$ خواهد بود. در این حالت ما عاملی را به دست نمیآوریم. بنابراین، سعی میکنیم در حین محاسبهٔ $M$، عمل $\gcd$ را چندین بار انجام دهیم.
برخی از اعداد مرکب عاملی مانند $p$ ندارند که $p-1$ برای $\mathrm{B}$ کوچک، $\mathrm{B}$-powersmooth باشد. برای مثال، برای عدد مرکب $100~000~000~000~000~493 = 763~013 \cdot 131~059~365~961$، مقادیر $p-1$ به ترتیب $190~753$-powersmooth و $1~092~161~383$-powersmooth هستند. برای تجزیهٔ این عدد مجبور خواهیم بود $B \geq 190~753$ را انتخاب کنیم.
در پیادهسازی زیر ما با $\mathrm{B} = 10$ شروع میکنیم و پس از هر تکرار $\mathrm{B}$ را افزایش میدهیم.
long long pollards_p_minus_1(long long n) {
int B = 10;
long long g = 1;
while (B <= 1000000 && g < n) {
long long a = 2 + rand() % (n - 3);
g = gcd(a, n);
if (g > 1)
return g;
// compute a^M
for (int p : primes) {
if (p >= B)
continue;
long long p_power = 1;
while (p_power * p <= B)
p_power *= p;
a = power(a, p_power, n);
g = gcd(a - 1, n);
if (g > 1 && g < n)
return g;
}
B *= 2;
}
return 1;
}
توجه داشته باشید که این یک الگوریتم احتمالی است. نتیجهٔ این امر این است که این احتمال وجود دارد که الگوریتم اصلاً نتواند عاملی پیدا کند.
پیچیدگی زمانی $O(B \log B \log^2 n)$ در هر تکرار است.
الگوریتم rho پولارد¶
الگوریتم Rho پولارد یکی دیگر از الگوریتمهای تجزیه از جان پولارد است.
فرض کنید تجزیهٔ به عوامل اول یک عدد به صورت $n = p q$ باشد. این الگوریتم یک دنبالهٔ شبهتصادفی $\{x_i\} = \{x_0,~f(x_0),~f(f(x_0)),~\dots\}$ را بررسی میکند که در آن $f$ یک تابع چندجملهای است، و معمولاً $f(x) = (x^2 + c) \bmod n$ با $c = 1$ انتخاب میشود.
در این مورد، ما به دنبالهٔ $\{x_i\}$ علاقهای نداریم. ما بیشتر به دنبالهٔ $\{x_i \bmod p\}$ علاقهمندیم. از آنجایی که $f$ یک تابع چندجملهای است و تمام مقادیر در بازهٔ $[0;~p)$ قرار دارند، این دنباله در نهایت به یک حلقه همگرا میشود. در واقع، پارادوکس روز تولد نشان میدهد که تعداد عناصر مورد انتظار تا شروع تکرار، $O(\sqrt{p})$ است. اگر $p$ کوچکتر از $\sqrt{n}$ باشد، تکرار به احتمال زیاد در $O(\sqrt[4]{n})$ شروع خواهد شد.
در اینجا یک تصویرسازی از چنین دنبالهای $\{x_i \bmod p\}$ با $n = 2206637$ و $p = 317$ و $x_0 = 2$ و $f(x) = x^2 + 1$ آمده است. از شکل دنباله میتوانید به وضوح ببینید که چرا این الگوریتم، الگوریتم $\rho$ پولارد نامیده میشود.
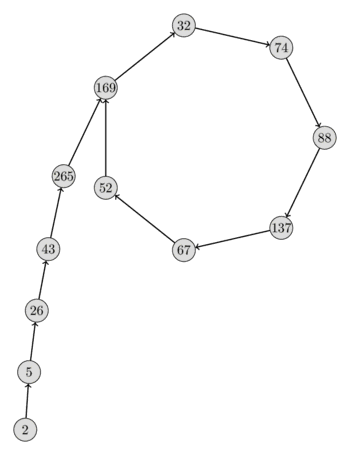
با این حال، هنوز یک سؤال باز وجود دارد. چگونه میتوانیم از ویژگیهای دنبالهٔ $\{x_i \bmod p\}$ به نفع خودمان استفاده کنیم، بدون اینکه حتی خود عدد $p$ را بدانیم؟
در واقع بسیار آسان است. در دنبالهٔ $\{x_i \bmod p\}_{i \le j}$ یک حلقه وجود دارد اگر و تنها اگر دو اندیس $s, t \le j$ وجود داشته باشند به طوری که $x_s \equiv x_t \bmod p$ باشد. این معادله را میتوان به صورت $x_s - x_t \equiv 0 \bmod p$ بازنویسی کرد، که به این معناست که $p$ یک مقسومعلیه $x_s-x_t$ است. از آنجایی که $p$ مقسومعلیه $n$ نیز هست، نتیجه میشود که $p | \gcd(x_s - x_t, n)$.
بنابراین، اگر دو اندیس $s$ و $t$ با $g = \gcd(x_s - x_t, n) > 1$ پیدا کنیم، یک حلقه و همچنین یک عامل $g$ از $n$ را پیدا کردهایم. این امکان وجود دارد که $g = n$ باشد. در این حالت ما یک عامل سره پیدا نکردهایم، بنابراین باید الگوریتم را با یک پارامتر متفاوت (مقدار شروع متفاوت $x_0$، ثابت متفاوت $c$ در تابع چندجملهای $f$) تکرار کنیم.
برای پیدا کردن حلقه، میتوانیم از هر الگوریتم رایج تشخیص حلقه استفاده کنیم.
الگوریتم تشخیص حلقه فلوید¶
این الگوریتم با استفاده از دو اشارهگر که با سرعتهای متفاوت روی دنباله حرکت میکنند، یک حلقه را پیدا میکند. در طول هر تکرار، اشارهگر اول یک عنصر به جلو میرود، در حالی که اشارهگر دوم دو عنصر به جلو میرود. با استفاده از این ایده به راحتی میتوان مشاهده کرد که اگر حلقهای وجود داشته باشد، در نقطهای اشارهگر دوم در طی حلقهها به اشارهگر اول میرسد. اگر طول حلقه $\lambda$ و $\mu$ اولین اندیسی باشد که حلقه در آن شروع میشود، آنگاه الگوریتم در زمان $O(\lambda + \mu)$ اجرا میشود.
این الگوریتم به الگوریتم لاکپشت و خرگوش نیز معروف است، که بر اساس داستانی است که در آن یک لاکپشت (اشارهگر کند) و یک خرگوش (اشارهگر سریعتر) مسابقه میدهند.
در واقع با استفاده از این الگوریتم میتوان پارامترهای $\lambda$ و $\mu$ را نیز تعیین کرد (همچنین در زمان $O(\lambda + \mu)$ و فضای $O(1)$). هنگامی که یک حلقه شناسایی شود، الگوریتم 'True' را برمیگرداند. اگر دنباله حلقه نداشته باشد، تابع به طور بیپایان حلقه میزند. با این حال، با استفاده از الگوریتم Rho پولارد، میتوان از این امر جلوگیری کرد.
function floyd(f, x0):
tortoise = x0
hare = f(x0)
while tortoise != hare:
tortoise = f(tortoise)
hare = f(f(hare))
return true
پیادهسازی¶
ابتدا، در اینجا یک پیادهسازی با استفاده از الگوریتم تشخیص حلقه فلوید آورده شده است. این الگوریتم به طور کلی در زمان $O(\sqrt[4]{n} \log(n))$ اجرا میشود.
long long mult(long long a, long long b, long long mod) {
return (__int128)a * b % mod;
}
long long f(long long x, long long c, long long mod) {
return (mult(x, x, mod) + c) % mod;
}
long long rho(long long n, long long x0=2, long long c=1) {
long long x = x0;
long long y = x0;
long long g = 1;
while (g == 1) {
x = f(x, c, n);
y = f(y, c, n);
y = f(y, c, n);
g = gcd(abs(x - y), n);
}
return g;
}
جدول زیر مقادیر $x$ و $y$ را در طول اجرای الگوریتم برای $n = 2206637$ و $x_0 = 2$ و $c = 1$ نشان میدهد.
این پیادهسازی از یک تابع mult استفاده میکند که دو عدد صحیح $\le 10^{18}$ را بدون سرریز شدن ضرب میکند. این کار با استفاده از نوع داده __int128 کامپایلر GCC برای اعداد صحیح ۱۲۸ بیتی انجام میشود.
اگر GCC در دسترس نباشد، میتوانید از ایدهای مشابه با توانرسانی دودویی استفاده کنید.
long long mult(long long a, long long b, long long mod) {
long long result = 0;
while (b) {
if (b & 1)
result = (result + a) % mod;
a = (a + a) % mod;
b >>= 1;
}
return result;
}
به عنوان جایگزین، میتوانید ضرب مونتگومری را نیز پیادهسازی کنید.
همانطور که قبلاً گفته شد، اگر $n$ مرکب باشد و الگوریتم $n$ را به عنوان عامل برگرداند، باید رویه را با پارامترهای متفاوت $x_0$ و $c$ تکرار کنید. برای مثال، انتخاب $x_0 = c = 1$ عدد $25 = 5 \cdot 5$ را تجزیه نخواهد کرد. الگوریتم عدد $25$ را برمیگرداند. با این حال، انتخاب $x_0 = 1$ و $c = 2$ آن را تجزیه خواهد کرد.
الگوریتم برنت¶
برنت روشی مشابه فلوید با استفاده از دو اشارهگر پیادهسازی میکند. تفاوت در این است که به جای پیش بردن اشارهگرها به ترتیب به اندازه یک و دو مکان، آنها به اندازه توانهای دو به جلو برده میشوند. به محض اینکه $2^i$ از $\lambda$ و $\mu$ بزرگتر شود، حلقه را پیدا خواهیم کرد.
function floyd(f, x0):
tortoise = x0
hare = f(x0)
l = 1
while tortoise != hare:
tortoise = hare
repeat l times:
hare = f(hare)
if tortoise == hare:
return true
l *= 2
return true
الگوریتم برنت نیز در زمان خطی اجرا میشود، اما به طور کلی سریعتر از فلوید است، زیرا از تعداد کمتری ارزیابی تابع $f$ استفاده میکند.
پیادهسازی¶
پیادهسازی مستقیم الگوریتم برنت را میتوان با حذف جملات $x_l - x_k$ در صورتی که $k < \frac{3 \cdot l}{2}$ باشد، سرعت بخشید. علاوه بر این، به جای انجام محاسبهٔ $\gcd$ در هر مرحله، ما جملات را در هم ضرب میکنیم و تنها هر چند مرحله یکبار $\gcd$ را بررسی میکنیم و در صورت عبور از عامل، به عقب برمیگردیم.
long long brent(long long n, long long x0=2, long long c=1) {
long long x = x0;
long long g = 1;
long long q = 1;
long long xs, y;
int m = 128;
int l = 1;
while (g == 1) {
y = x;
for (int i = 1; i < l; i++)
x = f(x, c, n);
int k = 0;
while (k < l && g == 1) {
xs = x;
for (int i = 0; i < m && i < l - k; i++) {
x = f(x, c, n);
q = mult(q, abs(y - x), n);
}
g = gcd(q, n);
k += m;
}
l *= 2;
}
if (g == n) {
do {
xs = f(xs, c, n);
g = gcd(abs(xs - y), n);
} while (g == 1);
}
return g;
}
ترکیب تقسیم آزمایشی برای اعداد اول کوچک به همراه نسخهٔ برنت از الگوریتم rho پولارد، یک الگوریتم تجزیهٔ بسیار قدرتمند را میسازد.