پایینترین جد مشترک - الگوریتم فاراک-کالتون و بِندِر¶
فرض کنید $G$ یک درخت باشد. برای هر پرسوجو به شکل $(u, v)$، ما میخواهیم پایینترین جد مشترک گرههای $u$ و $v$ را پیدا کنیم، یعنی میخواهیم گره $w$ را بیابیم که هم در مسیر از $u$ به ریشه و هم در مسیر از $v$ به ریشه قرار داشته باشد، و اگر چندین گره با این ویژگی وجود داشت، آنی را انتخاب میکنیم که از گره ریشه دورتر است. به عبارت دیگر، گره $w$ مورد نظر، پایینترین جد $u$ و $v$ است. به طور خاص، اگر $u$ جد $v$ باشد، آنگاه $u$ پایینترین جد مشترک آنها است.
الگوریتمی که در این مقاله شرح داده میشود توسط فاراک-کالتون و بِندِر توسعه داده شده است. این الگوریتم از نظر مجانبی بهینه است.
الگوریتم¶
ما از روش کلاسیک کاهش مسئله LCA به مسئله RMQ استفاده میکنیم. ما تمام گرههای درخت را با DFS پیمایش میکنیم و آرایهای از تمام گرههای بازدید شده و ارتفاع این گرهها را نگهداری میکنیم. پایینترین جد مشترک دو گره $u$ و $v$، گرهی است که بین رخدادهای $u$ و $v$ در پیمایش قرار دارد و کمترین ارتفاع را دارد.
در تصویر زیر میتوانید یک پیمایش اویلر ممکن برای یک گراف را ببینید و در لیست زیر آن، گرههای بازدید شده و ارتفاع آنها را مشاهده کنید.
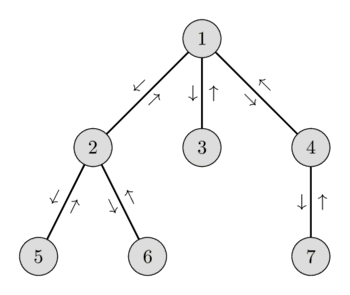
شما میتوانید درباره این کاهش در مقاله پایینترین جد مشترک بیشتر بخوانید. در آن مقاله، کمینه یک بازه یا با روش تجزیه جذر مربعی در $O(\sqrt{N})$ یا با استفاده از یک Segment tree در $O(\log N)$ پیدا میشد. در این مقاله، ما بررسی میکنیم که چگونه میتوانیم پرسوجوهای کمینه بازه (range minimum queries) داده شده را در زمان $O(1)$ حل کنیم، در حالی که برای پیشپردازش همچنان فقط زمان $O(N)$ صرف میشود.
توجه داشته باشید که مسئله RMQ کاهشیافته بسیار خاص است: هر دو عنصر مجاور در آرایه دقیقاً یک واحد با هم اختلاف دارند (زیرا عناصر آرایه چیزی جز ارتفاع گرههای بازدید شده به ترتیب پیمایش نیستند، و ما یا به یک فرزند میرویم که در این صورت عنصر بعدی یک واحد بزرگتر است، یا به جد برمیگردیم که در این صورت عنصر بعدی یک واحد کوچکتر است). الگوریتم فاراک-کالتون و بِندِر راه حلی دقیقاً برای همین مسئله خاص RMQ ارائه میدهد.
فرض کنید $A$ آرایهای باشد که میخواهیم پرسوجوهای کمینه بازه را روی آن انجام دهیم. و $N$ اندازه $A$ خواهد بود.
یک ساختمان داده ساده وجود دارد که میتوانیم برای حل مسئله RMQ با پیشپردازش $O(N \log N)$ و $O(1)$ برای هر پرسوجو از آن استفاده کنیم: جدول پراکنده (Sparse Table). ما یک جدول $T$ میسازیم که در آن هر عنصر $T[i][j]$ برابر با کمینه آرایه $A$ در بازه $[i, i + 2^j - 1]$ است. بدیهی است که $0 \leq j \leq \lceil \log N \rceil$، و بنابراین اندازه Sparse Table برابر با $O(N \log N)$ خواهد بود. شما میتوانید این جدول را به راحتی در $O(N \log N)$ با توجه به این نکته بسازید که $T[i][j] = \min(T[i][j-1], T[i+2^{j-1}][j-1])$ است.
چگونه میتوانیم با استفاده از این ساختمان داده به یک پرسوجوی RMQ در $O(1)$ پاسخ دهیم؟ فرض کنید پرسوجوی دریافتی $[l, r]$ باشد، آنگاه پاسخ برابر است با $\min(T[l][\text{sz}], T[r-2^{\text{sz}}+1][\text{sz}])$، که در آن $\text{sz}$ بزرگترین توانی است به طوری که $2^{\text{sz}}$ از طول بازه $r-l+1$ بزرگتر نباشد. در واقع، میتوانیم بازه $[l, r]$ را با دو قطعه به طول $2^{\text{sz}}$ پوشش دهیم - یکی که از $l$ شروع میشود و دیگری که به $r$ ختم میشود. این قطعات با هم همپوشانی دارند، اما این موضوع در محاسبات ما تداخلی ایجاد نمیکند. برای رسیدن واقعی به پیچیدگی زمانی $O(1)$ برای هر پرسوجو، باید مقادیر $\text{sz}$ را برای تمام طولهای ممکن از $1$ تا $N$ بدانیم. اما این مقادیر را میتوان به راحتی پیشمحاسبه کرد.
حالا میخواهیم پیچیدگی پیشپردازش را به $O(N)$ کاهش دهیم.
ما آرایه $A$ را به بلوکهایی با اندازه $K = 0.5 \log N$ تقسیم میکنیم که در آن $\log$ لگاریتم در پایه 2 است. برای هر بلوک، عنصر کمینه را محاسبه کرده و آنها را در آرایهای به نام $B$ ذخیره میکنیم. $B$ اندازهای برابر $\frac{N}{K}$ دارد. ما یک sparse table از آرایه $B$ میسازیم. اندازه و پیچیدگی زمانی آن برابر خواهد بود با:
حالا فقط باید یاد بگیریم چگونه به سرعت به پرسوجوهای کمینه بازه در داخل هر بلوک پاسخ دهیم. در واقع اگر پرسوجوی کمینه بازه دریافتی $[l, r]$ باشد و $l$ و $r$ در بلوکهای متفاوتی باشند، آنگاه پاسخ، کمینه سه مقدار زیر است: کمینه پسوند بلوکِ $l$ که از $l$ شروع میشود، کمینه پیشوند بلوکِ $r$ که به $r$ ختم میشود، و کمینه بلوکهای بین این دو. کمینه بلوکهای میانی را میتوان با استفاده از Sparse Table در $O(1)$ پاسخ داد. بنابراین تنها پرسوجوهای کمینه بازه درون بلوکها باقی میمانند.
اینجا از ویژگی خاص آرایه استفاده خواهیم کرد. به یاد داشته باشید که مقادیر در آرایه - که همان مقادیر ارتفاع در درخت هستند - همیشه یک واحد با هم اختلاف دارند. اگر عنصر اول یک بلوک را حذف کنیم و آن را از هر آیتم دیگر در بلوک کم کنیم، هر بلوک را میتوان با یک دنباله به طول $K - 1$ متشکل از اعداد $+1$ و $-1$ شناسایی کرد. چون این بلوکها بسیار کوچک هستند، تنها تعداد کمی دنباله متفاوت میتواند رخ دهد. تعداد دنبالههای ممکن برابر است با:
بنابراین تعداد بلوکهای مختلف $O(\sqrt{N})$ است، و در نتیجه میتوانیم نتایج پرسوجوهای کمینه بازه را در داخل تمام بلوکهای مختلف در زمان $O(\sqrt{N} K^2) = O(\sqrt{N} \log^2(N)) = O(N)$ پیشمحاسبه کنیم. برای پیادهسازی، میتوانیم یک بلوک را با یک بیتماسک به طول $K-1$ مشخص کنیم (که در یک int استاندارد جا میشود) و اندیس کمینه را در یک آرایه $\text{block}[\text{mask}][l][r]$ با اندازه $O(\sqrt{N} \log^2(N))$ ذخیره کنیم.
بنابراین ما یاد گرفتیم چگونه پرسوجوهای کمینه بازه را در داخل هر بلوک و همچنین پرسوجوهای کمینه بازه روی بازهای از بلوکها را، همگی در $O(N)$ پیشمحاسبه کنیم.
با این پیشمحاسبات میتوانیم هر پرسوجو را در $O(1)$ پاسخ دهیم، با استفاده از حداکثر چهار مقدار پیشمحاسبه شده: کمینه بلوک حاوی l، کمینه بلوک حاوی r، و دو کمینه از بخشهای همپوشان بلوکهای بین آنها.
پیادهسازی¶
int n;
vector<vector<int>> adj;
int block_size, block_cnt;
vector<int> first_visit;
vector<int> euler_tour;
vector<int> height;
vector<int> log_2;
vector<vector<int>> st;
vector<vector<vector<int>>> blocks;
vector<int> block_mask;
void dfs(int v, int p, int h) {
first_visit[v] = euler_tour.size();
euler_tour.push_back(v);
height[v] = h;
for (int u : adj[v]) {
if (u == p)
continue;
dfs(u, v, h + 1);
euler_tour.push_back(v);
}
}
int min_by_h(int i, int j) {
return height[euler_tour[i]] < height[euler_tour[j]] ? i : j;
}
void precompute_lca(int root) {
// دریافت پیمایش اویلر و اندیس اولین رخدادها
first_visit.assign(n, -1);
height.assign(n, 0);
euler_tour.reserve(2 * n);
dfs(root, -1, 0);
// پیشمحاسبه تمام مقادیر لگاریتم
int m = euler_tour.size();
log_2.reserve(m + 1);
log_2.push_back(-1);
for (int i = 1; i <= m; i++)
log_2.push_back(log_2[i / 2] + 1);
block_size = max(1, log_2[m] / 2);
block_cnt = (m + block_size - 1) / block_size;
// پیشمحاسبه کمینه هر بلوک و ساختن sparse table
st.assign(block_cnt, vector<int>(log_2[block_cnt] + 1));
for (int i = 0, j = 0, b = 0; i < m; i++, j++) {
if (j == block_size)
j = 0, b++;
if (j == 0 || min_by_h(i, st[b][0]) == i)
st[b][0] = i;
}
for (int l = 1; l <= log_2[block_cnt]; l++) {
for (int i = 0; i < block_cnt; i++) {
int ni = i + (1 << (l - 1));
if (ni >= block_cnt)
st[i][l] = st[i][l-1];
else
st[i][l] = min_by_h(st[i][l-1], st[ni][l-1]);
}
}
// پیشمحاسبه ماسک برای هر بلوک
block_mask.assign(block_cnt, 0);
for (int i = 0, j = 0, b = 0; i < m; i++, j++) {
if (j == block_size)
j = 0, b++;
if (j > 0 && (i >= m || min_by_h(i - 1, i) == i - 1))
block_mask[b] += 1 << (j - 1);
}
// پیشمحاسبه RMQ برای هر بلوک منحصربهفرد
int possibilities = 1 << (block_size - 1);
blocks.resize(possibilities);
for (int b = 0; b < block_cnt; b++) {
int mask = block_mask[b];
if (!blocks[mask].empty())
continue;
blocks[mask].assign(block_size, vector<int>(block_size));
for (int l = 0; l < block_size; l++) {
blocks[mask][l][l] = l;
for (int r = l + 1; r < block_size; r++) {
blocks[mask][l][r] = blocks[mask][l][r - 1];
if (b * block_size + r < m)
blocks[mask][l][r] = min_by_h(b * block_size + blocks[mask][l][r],
b * block_size + r) - b * block_size;
}
}
}
}
int lca_in_block(int b, int l, int r) {
return blocks[block_mask[b]][l][r] + b * block_size;
}
int lca(int v, int u) {
int l = first_visit[v];
int r = first_visit[u];
if (l > r)
swap(l, r);
int bl = l / block_size;
int br = r / block_size;
if (bl == br)
return euler_tour[lca_in_block(bl, l % block_size, r % block_size)];
int ans1 = lca_in_block(bl, l % block_size, block_size - 1);
int ans2 = lca_in_block(br, 0, r % block_size);
int ans = min_by_h(ans1, ans2);
if (bl + 1 < br) {
int l = log_2[br - bl - 1];
int ans3 = st[bl+1][l];
int ans4 = st[br - (1 << l)][l];
ans = min_by_h(ans, min_by_h(ans3, ans4));
}
return euler_tour[ans];
}