پرش به محتویات

ترفند پوسته محدب و درخت لی چائو

مسئله زیر را در نظر بگیرید. تعداد $n$ شهر وجود دارد. شما می‌خواهید با ماشین از شهر ۱ به شهر $n$ سفر کنید. برای این کار باید مقداری بنزین بخرید. می‌دانیم که هزینه یک لیتر بنزین در شهر $k$-ام برابر $cost_k$ است. در ابتدا باک بنزین شما خالی است و در هر کیلومتر یک لیتر بنزین مصرف می‌کنید. شهرها به ترتیب صعودی روی یک خط قرار دارند و شهر $k$-ام دارای مختصات $x_k$ است. همچنین برای ورود به شهر $k$-ام باید $toll_k$ عوارض بپردازید. وظیفه شما این است که این سفر را با کمترین هزینه ممکن انجام دهید. واضح است که راه‌حل را می‌توان از طریق برنامه‌نویسی پویا محاسبه کرد:

$$dp_i = toll_i+\min\limits_{j<i}(cost_j \cdot (x_i - x_j)+dp_j)$$

رویکرد ساده پیچیدگی $O(n^2)$ خواهد داشت که می‌توان آن را به $O(n \log n)$ یا $O(n \log [C \varepsilon^{-1}])$ بهبود داد، که در آن $C$ بزرگترین مقدار ممکن برای $|x_i|$ و $\varepsilon$ دقتی است که $x_i$ با آن در نظر گرفته می‌شود (برای اعداد صحیح که معمولاً همین‌طور است، $\varepsilon = 1$ است). برای این کار، باید توجه داشت که مسئله را می‌توان به افزودن توابع خطی $k \cdot x + b$ به یک مجموعه و پیدا کردن کمترین مقدار این توابع در یک نقطه خاص $x$ کاهش داد. دو رویکرد اصلی برای این کار وجود دارد.

ترفند پوسته محدب (Convex hull trick)

ایده این رویکرد، نگهداری پوسته محدب پایینی توابع خطی است. در واقع، کمی راحت‌تر است که آن‌ها را نه به عنوان توابع خطی، بلکه به عنوان نقاط $(k;b)$ روی صفحه در نظر بگیریم به طوری که باید نقطه‌ای را پیدا کنیم که کمترین حاصل‌ضرب داخلی را با نقطه داده‌شده $(x;1)$ داشته باشد، یعنی برای آن نقطه، مقدار $kx+b$ کمینه شود که همان مسئله اولیه است. چنین کمینه‌ای لزوماً روی پوش محدب پایینی این نقاط قرار خواهد گرفت، همانطور که در زیر مشاهده می‌شود:

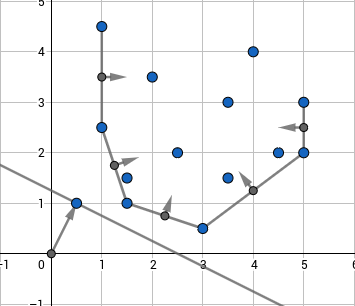
پوسته محدب پایینی

باید نقاط روی پوسته محدب و بردارهای نرمال یال‌های پوسته را نگهداری کرد. وقتی یک پرسش $(x;1)$ دارید، باید بردار نرمالی را پیدا کنید که از نظر زاویه به آن نزدیک‌ترین باشد، سپس تابع خطی بهینه به یکی از نقاط انتهایی آن یال متناظر خواهد بود. برای درک این موضوع، باید توجه داشت که نقاطی که حاصل‌ضرب داخلی ثابتی با $(x;1)$ دارند، روی خطی قرار می‌گیرند که بر $(x;1)$ عمود است، بنابراین تابع خطی بهینه، آنی خواهد بود که در آن، خط مماس بر پوسته محدب که با بردار عمود بر $(x;1)$ هم‌خط است، پوسته را لمس کند. این نقطه، نقطه‌ای است که بردارهای نرمال یال‌های سمت چپ و راست آن، در دو جهت مخالف نسبت به $(x;1)$ قرار دارند.

این رویکرد زمانی مفید است که پرسش‌های افزودن توابع خطی از نظر $k$ یکنوا باشند یا اگر به صورت آفلاین کار کنیم، یعنی می‌توانیم ابتدا تمام توابع خطی را اضافه کرده و سپس به پرسش‌ها پاسخ دهیم. بنابراین، نمی‌توانیم مسئله شهرها/بنزین را با این روش حل کنیم. این کار نیازمند مدیریت پرسش‌های آنلاین است. اما وقتی نوبت به مدیریت پرسش‌های آنلاین می‌رسد، کار سخت می‌شود و باید از نوعی ساختمان داده set برای پیاده‌سازی یک پوسته محدب مناسب استفاده کرد. با این حال، رویکرد آنلاین به دلیل سختی آن و اینکه رویکرد دوم (یعنی درخت لی چائو) اجازه می‌دهد مسئله به روشی بسیار ساده‌تر حل شود، در این مقاله بررسی نخواهد شد. شایان ذکر است که همچنان می‌توان از این رویکرد به صورت آنلاین و بدون پیچیدگی با استفاده از square-root-decomposition استفاده کرد. یعنی، هر $\sqrt n$ خط جدید، پوسته محدب را از ابتدا بازسازی کنیم.

برای پیاده‌سازی این رویکرد باید با چند تابع کمکی هندسی شروع کرد، در اینجا پیشنهاد می‌کنیم از نوع داده اعداد مختلط C++ استفاده کنید.

typedef int ftype;
typedef complex<ftype> point;
#define x real
#define y imag

ftype dot(point a, point b) {
    return (conj(a) * b).x();
}

ftype cross(point a, point b) {
    return (conj(a) * b).y();
}

در اینجا فرض می‌کنیم که هنگام افزودن توابع خطی، $k$ آن‌ها فقط افزایش می‌یابد و ما می‌خواهیم مقادیر کمینه را پیدا کنیم. ما نقاط را در یک وکتور hull و بردارهای نرمال را در وکتور vecs نگهداری می‌کنیم. وقتی یک نقطه جدید اضافه می‌کنیم، باید به زاویه‌ای که بین آخرین یال در پوسته محدب و بردار از آخرین نقطه در پوسته به نقطه جدید تشکیل می‌شود، نگاه کنیم. این زاویه باید در جهت پادساعتگرد باشد، یعنی حاصل‌ضرب داخلی آخرین بردار نرمال در پوسته (که به سمت داخل پوسته جهت‌دهی شده) و بردار از آخرین نقطه به نقطه جدید باید نامنفی باشد. تا زمانی که این شرط برقرار نباشد، باید آخرین نقطه در پوسته محدب را به همراه یال مربوطه حذف کنیم.

vector<point> hull, vecs;

void add_line(ftype k, ftype b) {
    point nw = {k, b};
    while(!vecs.empty() && dot(vecs.back(), nw - hull.back()) < 0) {
        hull.pop_back();
        vecs.pop_back();
    }
    if(!hull.empty()) {
        vecs.push_back(1i * (nw - hull.back()));
    }
    hull.push_back(nw);
}
حال برای به دست آوردن کمترین مقدار در یک نقطه، با استفاده از جستجوی دودویی، اولین بردار نرمال در پوسته محدب را پیدا می‌کنیم که بردار پرسش (x;1) نسبت به آن در جهت پادساعتگرد نباشد. نقطه شروع این یال، پاسخ بهینه خواهد بود. برای بررسی اینکه آیا بردار b نسبت به بردار a در جهت پادساعتگرد قرار دارد، باید مثبت بودن حاصل‌ضرب خارجی [a,b] را بررسی کنیم. 
int get(ftype x) {
    point query = {x, 1};
    auto it = lower_bound(vecs.begin(), vecs.end(), query, [](point a, point b) {
        return cross(a, b) > 0;
    });
    return dot(query, hull[it - vecs.begin()]);
}

درخت لی چائو (Li Chao tree)

فرض کنید مجموعه‌ای از توابع به شما داده شده است که هر دو تابع حداکثر یک بار یکدیگر را قطع می‌کنند. بیایید در هر رأس از یک درخت بازه‌ای یک تابع را به گونه‌ای نگهداری کنیم که اگر از ریشه به سمت یک برگ حرکت کنیم، تضمین شود که یکی از توابعی که در مسیر با آن روبرو شده‌ایم، تابعی باشد که کمترین مقدار را در آن برگ ایجاد می‌کند. بیایید ببینیم چگونه آن را بسازیم.

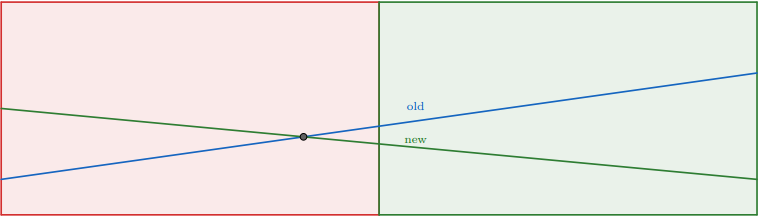
فرض کنید در رأسی هستیم که متناظر با نیم‌بازه $[l,r)$ است و تابع $f_{old}$ در آن نگهداری می‌شود و ما تابع $f_{new}$ را اضافه می‌کنیم. در این صورت، نقطه تقاطع یا در $[l,m)$ یا در $[m,r)$ خواهد بود که $m=\left\lfloor\tfrac{l+r}{2}\right\rfloor$ است. می‌توانیم با مقایسه مقادیر توابع در نقاط $l$ و $m$ به طور کارآمد این موضوع را بفهمیم. اگر تابع غالب تغییر کند، نقطه تقاطع در $[l,m)$ است، در غیر این صورت در $[m,r)$ قرار دارد. حال، برای نیمی از بازه که تقاطعی در آن نیست، تابع پایینی را انتخاب کرده و آن را در رأس فعلی می‌نویسیم. می‌توانید ببینید که این تابع همیشه همانی است که در نقطه $m$ پایین‌تر قرار دارد. پس از آن، به صورت بازگشتی با تابعی که بالاتر بود، به نیمه دیگر بازه می‌رویم. همانطور که می‌بینید، این کار درستی را در نیمه اول بازه حفظ می‌کند و در نیمه دیگر، درستی در طول فراخوانی بازگشتی حفظ خواهد شد. بنابراین می‌توانیم توابع را اضافه کرده و کمترین مقدار را در یک نقطه در زمان $O(\log [C\varepsilon^{-1}])$ بررسی کنیم.

در اینجا تصویری از آنچه در هنگام افزودن تابع جدید در یک رأس اتفاق می‌افتد، آمده است:

گره درخت لی چائو

حال به سراغ پیاده‌سازی برویم. یک بار دیگر از اعداد مختلط برای نگهداری توابع خطی استفاده خواهیم کرد.

typedef long long ftype;
typedef complex<ftype> point;
#define x real
#define y imag

ftype dot(point a, point b) {
    return (conj(a) * b).x();
}

ftype f(point a,  ftype x) {
    return dot(a, {x, 1});
}
ما توابع را در آرایه $line$ نگهداری می‌کنیم و از اندیس‌گذاری باینری برای درخت بازه‌ای استفاده می‌کنیم. اگر می‌خواهید از آن برای اعداد بزرگ یا اعداد اعشاری (double) استفاده کنید، باید از یک درخت بازه‌ای پویا (dynamic segment tree) استفاده کنید. درخت بازه‌ای باید با مقادیر پیش‌فرض مقداردهی اولیه شود، به عنوان مثال با خطوط $0x + \infty$.

const int maxn = 2e5;

point line[4 * maxn];

void add_line(point nw, int v = 1, int l = 0, int r = maxn) {
    int m = (l + r) / 2;
    bool lef = f(nw, l) < f(line[v], l);
    bool mid = f(nw, m) < f(line[v], m);
    if(mid) {
        swap(line[v], nw);
    }
    if(r - l == 1) {
        return;
    } else if(lef != mid) {
        add_line(nw, 2 * v, l, m);
    } else {
        add_line(nw, 2 * v + 1, m, r);
    }
}
حال برای به دست آوردن کمترین مقدار در یک نقطه $x$، به سادگی کمترین مقدار را در طول مسیر به سمت آن نقطه انتخاب می‌کنیم. 
ftype get(int x, int v = 1, int l = 0, int r = maxn) {
    int m = (l + r) / 2;
    if(r - l == 1) {
        return f(line[v], x);
    } else if(x < m) {
        return min(f(line[v], x), get(x, 2 * v, l, m));
    } else {
        return min(f(line[v], x), get(x, 2 * v + 1, m, r));
    }
}

مسائل