تجزیه سنگین-سبک (Heavy-light decomposition)¶
تجزیه سنگین-سبک (Heavy-light decomposition) یک تکنیک نسبتاً کلی است که به ما اجازه میدهد بسیاری از مسائلی را که به پرسوجو روی یک درخت خلاصه میشوند، به طور مؤثر حل کنیم.
شرح¶
درختی با $n$ رأس و یک ریشه دلخواه به نام $G$ را در نظر بگیرید.
ماهیت این تجزیه درخت، شکستن درخت به چندین مسیر است به طوری که بتوانیم از هر رأس $v$ با پیمایش حداکثر $\log n$ مسیر به رأس ریشه برسیم. علاوه بر این، هیچکدام از این مسیرها نباید با دیگری اشتراک داشته باشند.
واضح است که اگر چنین تجزیهای برای هر درختی پیدا کنیم، به ما این امکان را میدهد که برخی پرسوجوهای تکی از نوع «محاسبه چیزی روی مسیر از $a$ به $b$» را به چندین پرسوجو از نوع «محاسبه چیزی روی بازه $[l, r]$ از مسیر $k$-ام» کاهش دهیم.
الگوریتم ساخت¶
برای هر رأس $v$ اندازه زیردرخت آن، یعنی $s(v)$، را محاسبه میکنیم که همان تعداد رأسهای زیردرخت رأس $v$ به انضمام خود آن است.
سپس، تمام یالهایی را که از یک رأس $v$ به فرزندانش میروند در نظر میگیریم. یک یال را سنگین (heavy) مینامیم اگر به رأسی مانند $c$ برود به طوری که:
تمام یالهای دیگر سبک (light) نامیده میشوند.
بدیهی است که از هر رأس حداکثر یک یال سنگین میتواند به سمت پایین خارج شود، زیرا در غیر این صورت رأس $v$ حداقل دو فرزند با اندازه $\ge \frac{s(v)}{2}$ میداشت و در نتیجه اندازه زیردرخت $v$ بسیار بزرگ میشد، $s(v) \ge 1 + 2 \frac{s(v)}{2} > s(v)$، که به تناقض منجر میشود.
اکنون درخت را به مسیرهای مجزا تجزیه میکنیم. تمام رأسهایی را که هیچ یال سنگینی از آنها به پایین خارج نمیشود در نظر بگیرید. از هر کدام از این رأسها به سمت بالا حرکت میکنیم تا به ریشه درخت برسیم یا از یک یال سبک عبور کنیم. در نتیجه، چندین مسیر به دست میآوریم که از صفر یا چند یال سنگین به علاوه یک یال سبک تشکیل شدهاند. مسیری که به ریشه ختم میشود از این قاعده مستثناست و یال سبک نخواهد داشت. این مسیرها را مسیرهای سنگین (heavy paths) مینامیم - اینها همان مسیرهای مطلوب تجزیه سنگین-سبک هستند.
اثبات درستی¶
ابتدا، توجه میکنیم که مسیرهای سنگین به دست آمده توسط این الگوریتم، مجزا خواهند بود. در واقع، اگر دو مسیر از این نوع یک یال مشترک داشته باشند، به این معنی است که دو یال سنگین از یک رأس خارج شدهاند، که غیرممکن است.
دوم اینکه، نشان میدهیم که با حرکت از ریشه درخت به سمت پایین به یک رأس دلخواه، در طول مسیر بیش از $\log n$ بار مسیر سنگین را عوض نخواهیم کرد. حرکت به سمت پایین از طریق یک یال سبک، اندازه زیردرخت فعلی را به نصف یا کمتر کاهش میدهد:
بنابراین، ما میتوانیم حداکثر از $\log n$ یال سبک عبور کنیم تا اندازه زیردرخت به یک کاهش یابد.
از آنجایی که ما فقط میتوانیم از طریق یک یال سبک از یک مسیر سنگین به مسیر دیگر برویم (هر مسیر سنگین، به جز مسیری که از ریشه شروع میشود، یک یال سبک دارد)، ما نمیتوانیم در طول مسیر از ریشه به هر رأس، بیش از $\log n$ بار مسیر سنگین را عوض کنیم، همانطور که میخواستیم.
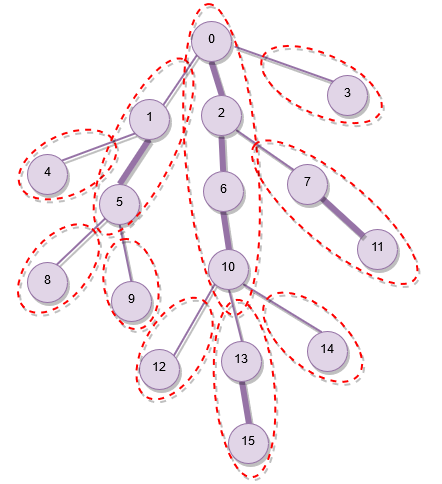
تصویر زیر تجزیه یک درخت نمونه را نشان میدهد. یالهای سنگین ضخیمتر از یالهای سبک هستند. مسیرهای سنگین با مرزهای نقطهچین مشخص شدهاند.
مسائل نمونه¶
هنگام حل مسائل، گاهی اوقات راحتتر است که تجزیه سنگین-سبک را به عنوان مجموعهای از مسیرهای مجزا از نظر رأس (به جای مجزا از نظر یال) در نظر بگیریم. برای این کار، کافی است که آخرین یال هر مسیر سنگین را، اگر سبک باشد، از آن حذف کنیم. در این صورت هیچ یک از ویژگیها نقض نمیشود، اما اکنون هر رأس دقیقاً به یک مسیر سنگین تعلق دارد.
در ادامه به برخی از مسائل نمونه که با کمک تجزیه سنگین-سبک قابل حل هستند، نگاهی میاندازیم.
به طور جداگانه، شایسته است به مسئله جمع اعداد روی یک مسیر توجه شود، زیرا این یک نمونه از مسائلی است که با تکنیکهای سادهتری نیز قابل حل است.
مقدار بیشینه در مسیر بین دو رأس¶
یک درخت داده شده است که به هر رأس آن مقداری تخصیص داده شده است. پرسوجوهایی از نوع $(a, b)$ وجود دارد که در آن $a$ و $b$ دو رأس در درخت هستند، و لازم است که مقدار بیشینه روی مسیر بین رأسهای $a$ و $b$ پیدا شود.
ما از قبل یک تجزیه سنگین-سبک از درخت میسازیم. روی هر مسیر سنگین یک درخت بازه (segment tree) میسازیم که به ما امکان میدهد رأسی با بیشترین مقدار تخصیص یافته را در یک بازه مشخص از یک مسیر سنگین مشخص در زمان $\mathcal{O}(\log n)$ پیدا کنیم. اگرچه تعداد مسیرهای سنگین در تجزیه سنگین-سبک میتواند به $n - 1$ برسد، اما اندازه کل همه مسیرها به $\mathcal{O}(n)$ محدود است، بنابراین اندازه کل درختهای بازه نیز خطی خواهد بود.
برای پاسخ به یک پرسوجوی $(a, b)$، پایینترین جد مشترک (LCA) $a$ و $b$ را به عنوان $l$ با هر روش دلخواهی پیدا میکنیم. اکنون مسئله به دو پرسوجوی $(a, l)$ و $(b, l)$ کاهش یافته است. برای هر یک از آنها میتوانیم این کار را انجام دهیم: مسیر سنگینی را که رأس پایینتر در آن قرار دارد پیدا کنیم، یک پرسوجو روی این مسیر انجام دهیم، به بالای این مسیر برویم، دوباره مشخص کنیم که در کدام مسیر سنگین هستیم و یک پرسوجو روی آن انجام دهیم، و به همین ترتیب ادامه دهیم تا به مسیری برسیم که شامل $l$ است.
باید مراقب حالتی بود که، برای مثال، $a$ و $l$ در یک مسیر سنگین قرار دارند - در این صورت پرسوجوی بیشینه روی این مسیر نباید روی هر پیشوندی انجام شود، بلکه باید روی بخش داخلی بین $a$ و $l$ انجام شود.
پاسخ به هر یک از زیرپرسوجوهای $(a, l)$ و $(b, l)$ نیازمند عبور از $\mathcal{O}(\log n)$ مسیر سنگین است و برای هر مسیر، یک پرسوجوی بیشینه روی بخشی از آن انجام میشود که خود به $\mathcal{O}(\log n)$ عملیات در درخت بازه نیاز دارد. از این رو، یک پرسوجوی $(a, b)$ زمان $\mathcal{O}(\log^2 n)$ میبرد.
اگر به طور اضافی بیشینه تمام پیشوندها را برای هر مسیر سنگین محاسبه و ذخیره کنید، به یک راهحل با پیچیدگی $\mathcal{O}(\log n)$ میرسید، زیرا تمام پرسوجوهای بیشینه روی پیشوندها هستند، به جز حداکثر یک بار زمانی که به جد مشترک $l$ میرسیم.
جمع اعداد در مسیر بین دو رأس¶
یک درخت داده شده است که به هر رأس آن مقداری تخصیص داده شده است. پرسوجوهایی از نوع $(a, b)$ وجود دارد که در آن $a$ و $b$ دو رأس در درخت هستند، و لازم است که جمع مقادیر روی مسیر بین رأسهای $a$ و $b$ پیدا شود. نوع دیگری از این مسئله نیز ممکن است که در آن علاوه بر این، عملیات بهروزرسانی وجود داشته باشد که عدد تخصیص داده شده به یک یا چند رأس را تغییر میدهد.
این مسئله را میتوان مشابه مسئله قبلی (بیشینه) با کمک تجزیه سنگین-سبک و با ساختن درختهای بازه روی مسیرهای سنگین حل کرد. اگر بهروزرسانی وجود نداشته باشد، میتوان به جای آن از مجموعهای پیشوندی استفاده کرد. با این حال، این مسئله با تکنیکهای سادهتری نیز قابل حل است.
اگر بهروزرسانی وجود نداشته باشد، میتوان جمع روی مسیر بین دو رأس را همزمان با جستجوی LCA دو رأس با استفاده از پرش دودویی (binary lifting) پیدا کرد — برای این کار، لازم است در کنار اجداد $2^k$-ام هر رأس، جمع مقادیر روی مسیرها تا آن اجداد را نیز در مرحله پیشپردازش ذخیره کنیم.
یک رویکرد اساساً متفاوت برای این مسئله وجود دارد - در نظر گرفتن گشت اویلر (Euler tour) درخت، و ساختن یک درخت بازه روی آن. این الگوریتم در مقالهای درباره یک مسئله مشابه بررسی شده است. باز هم، اگر بهروزرسانی وجود نداشته باشد، ذخیره کردن مجموعهای پیشوندی کافی است و نیازی به درخت بازه نیست.
هر دوی این روشها راهحلهای نسبتاً سادهای با پیچیدگی $\mathcal{O}(\log n)$ برای هر پرسوجو ارائه میدهند.
رنگآمیزی مجدد یالهای مسیر بین دو رأس¶
یک درخت داده شده است که هر یال آن در ابتدا سفید رنگ شده است. بهروزرسانیهایی از نوع $(a, b, c)$ وجود دارد، که در آن $a$ و $b$ دو رأس و $c$ یک رنگ است، که دستور میدهد تمام یالهای روی مسیر از $a$ به $b$ باید با رنگ $c$ دوباره رنگآمیزی شوند. پس از تمام رنگآمیزیها، لازم است گزارش شود که از هر رنگ چند یال به دست آمده است.
مشابه مسائل بالا، راهحل این است که به سادگی تجزیه سنگین-سبک را اعمال کرده و روی هر مسیر سنگین یک درخت بازه بسازیم.
هر رنگآمیزی مجدد روی مسیر $(a, b)$ به دو بهروزرسانی $(a, l)$ و $(b, l)$ تبدیل میشود، که در آن $l$ پایینترین جد مشترک رأسهای $a$ و $b$ است. $\mathcal{O}(\log n)$ به ازای هر مسیر برای $\mathcal{O}(\log n)$ مسیر، به پیچیدگی $\mathcal{O}(\log^2 n)$ برای هر بهروزرسانی منجر میشود.
پیادهسازی¶
بخشهای خاصی از رویکرد مورد بحث در بالا را میتوان برای آسانتر کردن پیادهسازی بدون از دست دادن کارایی، تغییر داد.
- تعریف یال سنگین را میتوان به یالی که به فرزندی با بزرگترین زیردرخت منتهی میشود تغییر داد، و در صورت برابر بودن اندازهها، انتخاب به صورت دلخواه است. این کار ممکن است منجر به تبدیل برخی یالهای سبک به سنگین شود، که به این معنی است که برخی مسیرهای سنگین با هم ترکیب شده و یک مسیر واحد را تشکیل میدهند، اما تمام مسیرهای سنگین همچنان مجزا باقی میمانند. همچنین هنوز تضمین میشود که حرکت به سمت پایین از طریق یک یال سبک، اندازه زیردرخت را به نصف یا کمتر کاهش میدهد.
- به جای ساختن یک درخت بازه برای هر مسیر سنگین، میتوان از یک درخت بازه واحد استفاده کرد که در آن بخشهای مجزا به هر مسیر سنگین اختصاص داده شده است.
- ذکر شد که پاسخ به پرسوجوها نیاز به محاسبه LCA دارد. در حالی که LCA را میتوان به طور جداگانه محاسبه کرد، امکان ادغام محاسبه LCA در فرآیند پاسخ به پرسوجوها نیز وجود دارد.
برای انجام تجزیه سنگین-سبک:
vector<int> parent, depth, heavy, head, pos;
int cur_pos;
int dfs(int v, vector<vector<int>> const& adj) {
int size = 1;
int max_c_size = 0;
for (int c : adj[v]) {
if (c != parent[v]) {
parent[c] = v, depth[c] = depth[v] + 1;
int c_size = dfs(c, adj);
size += c_size;
if (c_size > max_c_size)
max_c_size = c_size, heavy[v] = c;
}
}
return size;
}
void decompose(int v, int h, vector<vector<int>> const& adj) {
head[v] = h, pos[v] = cur_pos++;
if (heavy[v] != -1)
decompose(heavy[v], h, adj);
for (int c : adj[v]) {
if (c != parent[v] && c != heavy[v])
decompose(c, c, adj);
}
}
void init(vector<vector<int>> const& adj) {
int n = adj.size();
parent = vector<int>(n);
depth = vector<int>(n);
heavy = vector<int>(n, -1);
head = vector<int>(n);
pos = vector<int>(n);
cur_pos = 0;
dfs(0, adj);
decompose(0, 0, adj);
}
لیست مجاورت درخت باید به تابع init داده شود و تجزیه با فرض اینکه رأس 0 ریشه است، انجام میشود.
تابع dfs برای محاسبه heavy[v]، یعنی فرزندی که در انتهای دیگر یال سنگینِ خارج شده از v قرار دارد، برای هر رأس v استفاده میشود. علاوه بر این، dfs والدین و عمق هر رأس را نیز ذخیره میکند که بعداً در هنگام پرسوجوها مفید خواهد بود.
تابع decompose برای هر رأس v مقادیر head[v] و pos[v] را تخصیص میدهد که به ترتیب سرِ مسیر سنگینی که v به آن تعلق دارد و موقعیت v در درخت بازه واحدی است که تمام رأسها را پوشش میدهد.
برای پاسخ به پرسوجوها روی مسیرها، برای مثال پرسوجوی بیشینه که بحث شد، میتوانیم کاری شبیه به این انجام دهیم:
int query(int a, int b) {
int res = 0;
for (; head[a] != head[b]; b = parent[head[b]]) {
if (depth[head[a]] > depth[head[b]])
swap(a, b);
int cur_heavy_path_max = segment_tree_query(pos[head[b]], pos[b]);
res = max(res, cur_heavy_path_max);
}
if (depth[a] > depth[b])
swap(a, b);
int last_heavy_path_max = segment_tree_query(pos[a], pos[b]);
res = max(res, last_heavy_path_max);
return res;
}