مثلثبندی دلونی و دیاگرام ورونوی¶
مجموعهای از نقاط $\{p_i\}$ را در صفحه در نظر بگیرید. یک دیاگرام ورونوی $V(\{p_i\})$ از مجموعه $\{p_i\}$، افرازی از صفحه به $n$ ناحیه $V_i$ است، که در آن $V_i = \{p\in\mathbb{R}^2;\ \rho(p, p_i) = \min\ \rho(p, p_k)\}$ میباشد. سلولهای دیاگرام ورونوی چندضلعی (احتمالاً نامحدود) هستند. یک مثلثبندی دلونی $D(\{p_i\})$ از مجموعه $\{p_i\}$، یک مثلثبندی است که در آن هر نقطه $p_i$ خارج یا روی مرز دایره محیطی هر مثلث $T \in D(\{p_i\})$ قرار دارد.
یک حالت تبهگن ناخوشایند وجود دارد که در آن دیاگرام ورونوی همبند نیست و مثلثبندی دلونی وجود ندارد. این حالت زمانی رخ میدهد که تمام نقاط همخط باشند.
ویژگیها¶
مثلثبندی دلونی، کمینه زاویه را در بین تمام مثلثبندیهای ممکن، بیشینه میکند.
درخت پوشای کمینه اقلیدسی یک مجموعه نقطه، زیرمجموعهای از یالهای مثلثبندی دلونی آن است.
دوگانی¶
فرض کنید نقاط $\{p_i\}$ همخط نباشند و در بین $\{p_i\}$ هیچ چهار نقطهای روی یک دایره قرار نگیرند. در این صورت، $V(\{p_i\})$ و $D(\{p_i\})$ دوگان یکدیگرند، بنابراین اگر یکی از آنها را به دست آوریم، میتوانیم دیگری را در زمان $O(n)$ به دست آوریم. اگر این شرایط برقرار نباشد چه باید کرد؟ حالت همخط را میتوان به راحتی پردازش کرد. در غیر این صورت، $V$ و $D'$ دوگان هستند، که در آن $D'$ با حذف تمام یالهایی از $D$ به دست میآید که دو مثلث مجاور به آن یال، دایره محیطی مشترک داشته باشند.
ساختن دلونی و ورونوی¶
به دلیل وجود دوگانی، تنها به یک الگوریتم سریع برای محاسبه یکی از $V$ یا $D$ نیاز داریم. ما نحوه ساخت $D(\{p_i\})$ در زمان $O(n\log n)$ را توضیح خواهیم داد. این مثلثبندی از طریق الگوریتم تقسیم و حل ارائه شده توسط Guibas و Stolfi ساخته میشود.
ساختمان داده Quad-edge¶
در طول الگوریتم، $D$ درون ساختمان داده quad-edge ذخیره میشود. این ساختار در تصویر زیر شرح داده شده است:
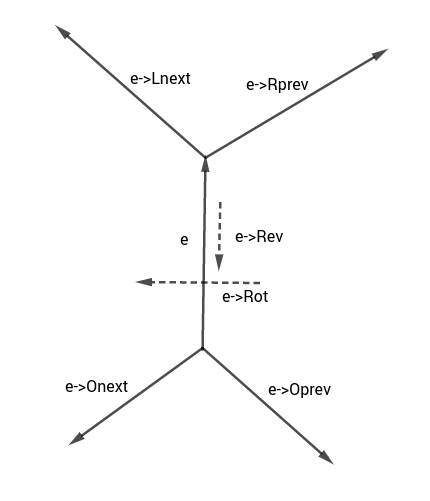
در الگوریتم از توابع زیر بر روی یالها استفاده خواهیم کرد:
make_edge(a, b)
این تابع یک یال مجزا از نقطهaبه نقطهbبه همراه یال معکوس و هر دو یال دوگان آن ایجاد میکند.splice(a, b)
این تابع، یک تابع کلیدی در الگوریتم است. این تابعa->Onextرا باb->Onextوa->Onext->Rot->Onextرا باb->Onext->Rot->Onextجابجا میکند.delete_edge(e)
این تابع یال e را از مثلثبندی حذف میکند. برای حذفe، میتوانیم به سادگیsplice(e, e->Oprev)وsplice(e->Rev, e->Rev->Oprev)را فراخوانی کنیم.connect(a, b)
این تابع یک یال جدیدeازa->Destبهb->Orgبه گونهای ایجاد میکند کهa،bوeهمگی وجه چپ یکسانی داشته باشند. برای این کار،e = make_edge(a->Dest, b->Org)،splice(e, a->Lnext)وsplice(e->Rev, b)را فراخوانی میکنیم.
الگوریتم¶
الگوریتم، مثلثبندی را محاسبه کرده و دو quad-edge را برمیگرداند: یال پوش محدب پادساعتگرد خروجی از چپترین رأس و یال پوش محدب ساعتگرد خروجی از راستترین رأس.
تمام نقاط را بر اساس مولفه x و در صورت تساوی بر اساس مولفه y مرتب میکنیم. مسئله را برای یک بازه $(l, r)$ (در ابتدا $(l, r) = (0, n - 1)$) حل میکنیم. اگر $r - l + 1 = 2$ باشد، یک یال $(p[l], p[r])$ اضافه کرده و برمیگردیم. اگر $r - l + 1 = 3$ باشد، ابتدا یالهای $(p[l], p[l + 1])$ و $(p[l + 1], p[r])$ را اضافه میکنیم. همچنین باید آنها را با استفاده از splice(a->Rev, b) به هم متصل کنیم. حالا باید مثلث را ببندیم. اقدام بعدی ما به جهتگیری نقاط $p[l]$، $p[l + 1]$ و $p[r]$ بستگی دارد. اگر همخط باشند، نمیتوانیم مثلث بسازیم، بنابراین به سادگی (a, b->Rev) را برمیگردانیم. در غیر این صورت، یک یال جدید c با فراخوانی connect(b, a) ایجاد میکنیم. اگر جهتگیری نقاط پادساعتگرد باشد، (a, b->Rev) را برمیگردانیم. در غیر این صورت، (c->Rev, c) را برمیگردانیم.
حال فرض کنید $r - l + 1 \ge 4$ باشد. ابتدا به صورت بازگشتی $L = (l, \frac{l + r}{2})$ و $R = (\frac{l + r}{2} + 1, r)$ را حل میکنیم. اکنون باید این دو مثلثبندی را در یک مثلثبندی واحد ادغام کنیم. توجه داشته باشید که نقاط ما مرتب شدهاند، بنابراین هنگام ادغام، یالهایی از L به R (که یالهای عرضی نامیده میشوند) اضافه کرده و برخی از یالهای L به L و R به R را حذف خواهیم کرد.
ساختار یالهای عرضی چگونه است؟ تمام این یالها باید خطی موازی با محور y را که در مقدار x جداکننده قرار دارد، قطع کنند. این امر یک ترتیب خطی برای یالهای عرضی ایجاد میکند، بنابراین میتوانیم در مورد یالهای عرضی متوالی، پایینترین یال عرضی و غیره صحبت کنیم. الگوریتم یالهای عرضی را به ترتیب صعودی اضافه میکند. توجه داشته باشید که هر دو یال عرضی مجاور یک نقطه پایانی مشترک خواهند داشت و ضلع سوم مثلثی که تعریف میکنند یا از L به L میرود یا از R به R. بیایید یال عرضی فعلی را یال پایه بنامیم. یال بعدیِ یال پایه یا از نقطه پایانی چپ یال پایه به یکی از همسایههای R نقطه پایانی راست میرود یا برعکس.
دایره محیطی یال پایه و یال عرضی قبلی را در نظر بگیرید. فرض کنید این دایره به دایرههای دیگری تبدیل میشود که یال پایه را به عنوان وتر دارند اما در جهت محور Oy بالاتر قرار میگیرند. دایره ما برای مدتی بالا میرود، اما مگر اینکه یال پایه مماس بالایی L و R باشد، به نقطهای برخورد خواهیم کرد که یا به L یا به R تعلق دارد و مثلث جدیدی را به وجود میآورد که هیچ نقطهای در دایره محیطی آن نیست. یال L-R جدید این مثلث، یال عرضی بعدی است که اضافه میشود. برای انجام این کار به صورت کارآمد، دو یال lcand و rcand را محاسبه میکنیم به طوری که lcand به اولین نقطه از L که در این فرآیند با آن مواجه میشویم اشاره میکند و rcand به اولین نقطه از R اشاره میکند. سپس آنی را انتخاب میکنیم که زودتر با آن مواجه شویم. در ابتدا یال پایه به مماس پایینی L و R اشاره میکند.
پیادهسازی¶
توجه داشته باشید که پیادهسازی تابع in_circle مختص کامپایلر GCC است.
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& a) { return a >= 0 ? a ? 1 : 0 : -1; }
struct pt {
ll x, y;
pt() { }
pt(ll _x, ll _y) : x(_x), y(_y) { }
pt operator-(const pt& p) const {
return pt(x - p.x, y - p.y);
}
ll cross(const pt& p) const {
return x * p.y - y * p.x;
}
ll cross(const pt& a, const pt& b) const {
return (a - *this).cross(b - *this);
}
ll dot(const pt& p) const {
return x * p.x + y * p.y;
}
ll dot(const pt& a, const pt& b) const {
return (a - *this).dot(b - *this);
}
ll sqrLength() const {
return this->dot(*this);
}
bool operator==(const pt& p) const {
return eq(x, p.x) && eq(y, p.y);
}
};
const pt inf_pt = pt(1e18, 1e18);
struct QuadEdge {
pt origin;
QuadEdge* rot = nullptr;
QuadEdge* onext = nullptr;
bool used = false;
QuadEdge* rev() const {
return rot->rot;
}
QuadEdge* lnext() const {
return rot->rev()->onext->rot;
}
QuadEdge* oprev() const {
return rot->onext->rot;
}
pt dest() const {
return rev()->origin;
}
};
QuadEdge* make_edge(pt from, pt to) {
QuadEdge* e1 = new QuadEdge;
QuadEdge* e2 = new QuadEdge;
QuadEdge* e3 = new QuadEdge;
QuadEdge* e4 = new QuadEdge;
e1->origin = from;
e2->origin = to;
e3->origin = e4->origin = inf_pt;
e1->rot = e3;
e2->rot = e4;
e3->rot = e2;
e4->rot = e1;
e1->onext = e1;
e2->onext = e2;
e3->onext = e4;
e4->onext = e3;
return e1;
}
void splice(QuadEdge* a, QuadEdge* b) {
swap(a->onext->rot->onext, b->onext->rot->onext);
swap(a->onext, b->onext);
}
void delete_edge(QuadEdge* e) {
splice(e, e->oprev());
splice(e->rev(), e->rev()->oprev());
delete e->rev()->rot;
delete e->rev();
delete e->rot;
delete e;
}
QuadEdge* connect(QuadEdge* a, QuadEdge* b) {
QuadEdge* e = make_edge(a->dest(), b->origin);
splice(e, a->lnext());
splice(e->rev(), b);
return e;
}
bool left_of(pt p, QuadEdge* e) {
return gt(p.cross(e->origin, e->dest()), 0);
}
bool right_of(pt p, QuadEdge* e) {
return lt(p.cross(e->origin, e->dest()), 0);
}
template <class T>
T det3(T a1, T a2, T a3, T b1, T b2, T b3, T c1, T c2, T c3) {
return a1 * (b2 * c3 - c2 * b3) - a2 * (b1 * c3 - c1 * b3) +
a3 * (b1 * c2 - c1 * b2);
}
bool in_circle(pt a, pt b, pt c, pt d) {
// اگر __int128 موجود باشد، مستقیماً محاسبه کنید.
// در غیر این صورت، زوایا را محاسبه کنید.
#if defined(__LP64__) || defined(_WIN64)
__int128 det = -det3<__int128>(b.x, b.y, b.sqrLength(), c.x, c.y,
c.sqrLength(), d.x, d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), c.x, c.y, c.sqrLength(), d.x,
d.y, d.sqrLength());
det -= det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), d.x,
d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), c.x,
c.y, c.sqrLength());
return det > 0;
#else
auto ang = [](pt l, pt mid, pt r) {
ll x = mid.dot(l, r);
ll y = mid.cross(l, r);
long double res = atan2((long double)x, (long double)y);
return res;
};
long double kek = ang(a, b, c) + ang(c, d, a) - ang(b, c, d) - ang(d, a, b);
if (kek > 1e-8)
return true;
else
return false;
#endif
}
pair<QuadEdge*, QuadEdge*> build_tr(int l, int r, vector<pt>& p) {
if (r - l + 1 == 2) {
QuadEdge* res = make_edge(p[l], p[r]);
return make_pair(res, res->rev());
}
if (r - l + 1 == 3) {
QuadEdge *a = make_edge(p[l], p[l + 1]), *b = make_edge(p[l + 1], p[r]);
splice(a->rev(), b);
int sg = sgn(p[l].cross(p[l + 1], p[r]));
if (sg == 0)
return make_pair(a, b->rev());
QuadEdge* c = connect(b, a);
if (sg == 1)
return make_pair(a, b->rev());
else
return make_pair(c->rev(), c);
}
int mid = (l + r) / 2;
QuadEdge *ldo, *ldi, *rdo, *rdi;
tie(ldo, ldi) = build_tr(l, mid, p);
tie(rdi, rdo) = build_tr(mid + 1, r, p);
while (true) {
if (left_of(rdi->origin, ldi)) {
ldi = ldi->lnext();
continue;
}
if (right_of(ldi->origin, rdi)) {
rdi = rdi->rev()->onext;
continue;
}
break;
}
QuadEdge* basel = connect(rdi->rev(), ldi);
auto valid = [&basel](QuadEdge* e) { return right_of(e->dest(), basel); };
if (ldi->origin == ldo->origin)
ldo = basel->rev();
if (rdi->origin == rdo->origin)
rdo = basel;
while (true) {
QuadEdge* lcand = basel->rev()->onext;
if (valid(lcand)) {
while (in_circle(basel->dest(), basel->origin, lcand->dest(),
lcand->onext->dest())) {
QuadEdge* t = lcand->onext;
delete_edge(lcand);
lcand = t;
}
}
QuadEdge* rcand = basel->oprev();
if (valid(rcand)) {
while (in_circle(basel->dest(), basel->origin, rcand->dest(),
rcand->oprev()->dest())) {
QuadEdge* t = rcand->oprev();
delete_edge(rcand);
rcand = t;
}
}
if (!valid(lcand) && !valid(rcand))
break;
if (!valid(lcand) ||
(valid(rcand) && in_circle(lcand->dest(), lcand->origin,
rcand->origin, rcand->dest())))
basel = connect(rcand, basel->rev());
else
basel = connect(basel->rev(), lcand->rev());
}
return make_pair(ldo, rdo);
}
vector<tuple<pt, pt, pt>> delaunay(vector<pt> p) {
sort(p.begin(), p.end(), [](const pt& a, const pt& b) {
return lt(a.x, b.x) || (eq(a.x, b.x) && lt(a.y, b.y));
});
auto res = build_tr(0, (int)p.size() - 1, p);
QuadEdge* e = res.first;
vector<QuadEdge*> edges = {e};
while (lt(e->onext->dest().cross(e->dest(), e->origin), 0))
e = e->onext;
auto add = [&p, &e, &edges]() {
QuadEdge* curr = e;
do {
curr->used = true;
p.push_back(curr->origin);
edges.push_back(curr->rev());
curr = curr->lnext();
} while (curr != e);
};
add();
p.clear();
int kek = 0;
while (kek < (int)edges.size()) {
if (!(e = edges[kek++])->used)
add();
}
vector<tuple<pt, pt, pt>> ans;
for (int i = 0; i < (int)p.size(); i += 3) {
ans.push_back(make_tuple(p[i], p[i + 1], p[i + 2]));
}
return ans;
}