درخت فنویک¶
فرض کنید $f$ یک عملگر گروهی باشد (یک تابع دودویی شرکتپذیر روی مجموعهای با یک عضو خنثی و اعضای وارون) و $A$ آرایهای از اعداد صحیح به طول $N$ باشد. نماد میانوندی $f$ را با $*$ نشان میدهیم؛ یعنی $f(x,y) = x*y$ برای اعداد صحیح دلخواه $x,y$. (از آنجایی که این عمل شرکتپذیر است، هنگام استفاده از نماد میانوندی، از پرانتز برای ترتیب اجرای $f$ صرفنظر میکنیم.)
درخت فنویک یک ساختمان داده است که:
- مقدار تابع $f$ را در بازه مشخص $[l, r]$ (یعنی $A_l * A_{l+1} * \dots * A_r$) در زمان $O(\log N)$ محاسبه میکند.
- مقدار یک عنصر از $A$ را در زمان $O(\log N)$ بهروزرسانی میکند.
- به حافظه $O(N)$ نیاز دارد (همان مقداری که برای $A$ لازم است).
- استفاده و پیادهسازی آن آسان است، به خصوص در مورد آرایههای چند بعدی.
رایجترین کاربرد درخت فنویک، محاسبه مجموع یک بازه است. برای مثال، با استفاده از عمل جمع روی مجموعه اعداد صحیح به عنوان عملگر گروهی، یعنی $f(x,y) = x + y$: عملگر دودویی $*$ در این حالت $+$ است، بنابراین $A_l * A_{l+1} * \dots * A_r = A_l + A_{l+1} + \dots + A_{r}$.
درخت فنویک با نام درخت اندیسگذاری شده دودویی (Binary Indexed Tree یا BIT) نیز شناخته میشود. این ساختار داده برای اولین بار در مقالهای با عنوان «یک ساختار داده جدید برای جداول فراوانی تجمعی» (Peter M. Fenwick، 1994) توصیف شد.
توضیحات¶
نمای کلی¶
برای سادگی، فرض میکنیم که تابع $f$ به صورت $f(x,y) = x + y$ روی اعداد صحیح تعریف شده است.
فرض کنید یک آرایه از اعداد صحیح $A[0 \dots N-1]$ به ما داده شده است. (توجه داشته باشید که از اندیسگذاری از صفر استفاده میکنیم.) درخت فنویک تنها یک آرایه $T[0 \dots N-1]$ است که در آن هر عنصر برابر با مجموع عناصر $A$ در یک بازه مشخص $[g(i), i]$ است:
که در آن $g$ تابعی است که در شرط $0 \le g(i) \le i$ صدق میکند. ما $g$ را در چند پاراگراف بعدی تعریف خواهیم کرد.
این ساختار داده به این دلیل درخت نامیده میشود که نمایش زیبایی از آن به شکل یک درخت وجود دارد، هرچند نیازی به مدلسازی یک درخت واقعی با گرهها و یالها نداریم. ما فقط باید آرایه $T$ را برای پاسخ به تمام پرسوجوها نگهداری کنیم.
نکته: درخت فنویک ارائهشده در اینجا از اندیسگذاری از صفر استفاده میکند. بسیاری از افراد از نسخهای از درخت فنویک استفاده میکنند که بر پایه اندیسگذاری از یک است. به همین دلیل، در بخش پیادهسازی، یک پیادهسازی جایگزین که از اندیسگذاری از یک استفاده میکند نیز خواهید یافت. هر دو نسخه از نظر پیچیدگی زمانی و حافظه معادل هستند.
اکنون میتوانیم شبهکدی برای دو عملیات ذکر شده بنویسیم. در زیر، ما مجموع عناصر $A$ در بازه $[0, r]$ را به دست میآوریم و یک عنصر $A_i$ را بهروزرسانی (افزایش) میکنیم:
تابع sum(عدد صحیح r):
نتیجه = 0
تا زمانی که (r >= 0):
نتیجه += t[r]
r = g(r) - 1
بازگرداندن نتیجه
تابع increase(عدد صحیح i, عدد صحیح delta):
برای تمام j هایی که g(j) <= i <= j:
t[j] += delta
تابع sum به این صورت کار میکند:
- ابتدا، مجموع بازه $[g(r), r]$ (یعنی $T[r]$) را به
resultاضافه میکند. - سپس به بازه $[g(g(r)-1), g(r)-1]$ «پرش» میکند و مجموع این بازه را به
resultاضافه میکند. - این کار تا زمانی ادامه مییابد که از بازه $[0, g(g( \dots g(r)-1 \dots -1)-1)]$ به بازه $[g(-1), -1]$ «پرش» کند؛ اینجا جایی است که تابع
sumمتوقف میشود.
تابع increase با منطق مشابهی کار میکند، اما در جهت افزایش اندیسها «پرش» میکند:
- مجموع برای هر بازه به شکل $[g(j), j]$ که در شرط $g(j) \le i \le j$ صدق کند، به اندازه
deltaافزایش مییابد؛ یعنیt[j] += delta. بنابراین، این تابع تمام عناصری از $T$ را که متناظر با بازههایی هستند که $A_i$ در آنها قرار دارد، بهروزرسانی میکند.
پیچیدگی هر دو تابع sum و increase به تابع $g$ بستگی دارد.
راههای زیادی برای انتخاب تابع $g$ وجود دارد به طوری که برای تمام $i$ها، $0 \le g(i) \le i$ باشد.
برای مثال، تابع $g(i) = i$ کار میکند که نتیجه آن $T = A$ خواهد بود (در این حالت، پرسوجوهای جمع کند هستند).
همچنین میتوانیم تابع $g(i) = 0$ را در نظر بگیریم.
این معادل آرایههای مجموع پیشوندی خواهد بود (در این حالت، یافتن مجموع بازه $[0, i]$ فقط زمان ثابت میبرد؛ اما بهروزرسانیها کند هستند).
بخش هوشمندانه الگوریتم درخت فنویک در نحوه استفاده از یک تعریف خاص برای تابع $g$ است که میتواند هر دو عملیات را در زمان $O(\log N)$ انجام دهد.
تعریف ¶
محاسبه $g(i)$ با استفاده از یک عملیات ساده تعریف میشود: ما تمام بیتهای ۱ انتهایی در نمایش دودویی $i$ را با بیتهای ۰ جایگزین میکنیم.
به عبارت دیگر، اگر کمارزشترین بیت $i$ در مبنای دو، ۰ باشد، آنگاه $g(i) = i$ است. در غیر این صورت، کمارزشترین بیت ۱ است و ما این ۱ و تمام بیتهای ۱ انتهایی دیگر را برعکس میکنیم.
برای مثال داریم:
یک پیادهسازی ساده با استفاده از عملیات بیتی برای عملیات غیربدیهی توصیف شده در بالا وجود دارد:
که در آن $\&$ عملگر AND بیتی است. متقاعد کردن خودتان مبنی بر اینکه این راهحل همان کار عملیات توصیف شده در بالا را انجام میدهد، دشوار نیست.
اکنون، فقط باید راهی برای پیمایش تمام $j$هایی پیدا کنیم که $g(j) \le i \le j$ باشد.
به راحتی میتوان دید که با شروع از $i$ و برعکس کردن آخرین بیت تنظیمنشده (unset)، میتوانیم تمام این $j$ها را پیدا کنیم. ما این عملیات را $h(j)$ مینامیم. برای مثال، برای $i = 10$ داریم:
جای تعجب نیست که یک راه ساده برای انجام $h$ با استفاده از عملیات بیتی نیز وجود دارد:
که در آن $|$ عملگر OR بیتی است.
تصویر زیر یک تفسیر ممکن از درخت فنویک به عنوان یک درخت را نشان میدهد. گرههای درخت، بازههایی را که پوشش میدهند، نمایش میدهند.
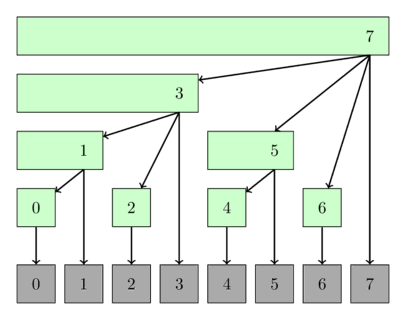
پیادهسازی¶
پیدا کردن مجموع در آرایه یکبعدی¶
در اینجا پیادهسازی درخت فنویک برای پرسوجوهای مجموع و بهروزرسانیهای تکی را ارائه میدهیم.
درخت فنویک معمولی فقط میتواند به پرسوجوهای مجموع از نوع $[0, r]$ با استفاده از sum(int r) پاسخ دهد، اما ما میتوانیم با محاسبه دو مجموع $[0, r]$ و $[0, l-1]$ و کم کردن آنها از یکدیگر، به پرسوجوهای نوع $[l, r]$ نیز پاسخ دهیم.
این کار در متد sum(int l, int r) انجام میشود.
همچنین این پیادهسازی از دو سازنده (constructor) پشتیبانی میکند. میتوانید یک درخت فنویک که با صفر مقداردهی اولیه شده است بسازید، یا یک آرایه موجود را به فرم فنویک تبدیل کنید.
struct FenwickTree {
vector<int> bit; // درخت اندیسگذاری شده دودویی
int n;
FenwickTree(int n) {
this->n = n;
bit.assign(n, 0);
}
FenwickTree(vector<int> const &a) : FenwickTree(a.size()) {
for (size_t i = 0; i < a.size(); i++)
add(i, a[i]);
}
int sum(int r) {
int ret = 0;
for (; r >= 0; r = (r & (r + 1)) - 1)
ret += bit[r];
return ret;
}
int sum(int l, int r) {
return sum(r) - sum(l - 1);
}
void add(int idx, int delta) {
for (; idx < n; idx = idx | (idx + 1))
bit[idx] += delta;
}
};
ساخت خطی¶
پیادهسازی بالا به زمان $O(N \log N)$ نیاز دارد. امکان بهبود آن به زمان $O(N)$ وجود دارد.
ایده این است که عدد $a[i]$ در اندیس $i$ به بازه ذخیره شده در $bit[i]$ و به تمام بازههایی که اندیس $i | (i + 1)$ به آنها کمک میکند، اضافه خواهد شد. بنابراین با اضافه کردن اعداد به ترتیب، فقط کافی است مجموع فعلی را به بازه بعدی منتقل کنید، که در آنجا دوباره به بازه بعدی منتقل میشود و به همین ترتیب ادامه مییابد.
FenwickTree(vector<int> const &a) : FenwickTree(a.size()){
for (int i = 0; i < n; i++) {
bit[i] += a[i];
int r = i | (i + 1);
if (r < n) bit[r] += bit[i];
}
}
پیدا کردن کمینه بازه در آرایه یکبعدی¶
واضح است که راه آسانی برای پیدا کردن کمینه بازه $[l, r]$ با استفاده از درخت فنویک وجود ندارد، زیرا درخت فنویک فقط میتواند به پرسوجوهای نوع $[0, r]$ پاسخ دهد.
علاوه بر این، هر بار که یک مقدار update میشود، مقدار جدید باید کوچکتر از مقدار فعلی باشد.
هر دوی این محدودیتهای قابل توجه به این دلیل است که عملگر $min$ به همراه مجموعه اعداد صحیح، یک گروه را تشکیل نمیدهد، زیرا عناصر وارون وجود ندارند.
struct FenwickTreeMin {
vector<int> bit;
int n;
const int INF = (int)1e9;
FenwickTreeMin(int n) {
this->n = n;
bit.assign(n, INF);
}
FenwickTreeMin(vector<int> a) : FenwickTreeMin(a.size()) {
for (size_t i = 0; i < a.size(); i++)
update(i, a[i]);
}
int getmin(int r) {
int ret = INF;
for (; r >= 0; r = (r & (r + 1)) - 1)
ret = min(ret, bit[r]);
return ret;
}
void update(int idx, int val) {
for (; idx < n; idx = idx | (idx + 1))
bit[idx] = min(bit[idx], val);
}
};
توجه: امکان پیادهسازی یک درخت فنویک وجود دارد که بتواند پرسوجوهای کمینه بازهای دلخواه و بهروزرسانیهای دلخواه را مدیریت کند. مقاله Efficient Range Minimum Queries using Binary Indexed Trees چنین رویکردی را توصیف میکند. با این حال، در آن رویکرد شما نیاز به نگهداری یک درخت اندیسگذاری شده دودویی دوم روی دادهها با ساختاری کمی متفاوت دارید، زیرا یک درخت برای ذخیره مقادیر تمام عناصر آرایه کافی نیست. پیادهسازی آن نیز در مقایسه با پیادهسازی معمولی برای مجموع، بسیار دشوارتر است.
پیدا کردن مجموع در آرایه دوبعدی¶
همانطور که قبلاً ادعا شد، پیادهسازی درخت فنویک برای آرایه چند بعدی بسیار آسان است.
struct FenwickTree2D {
vector<vector<int>> bit;
int n, m;
// init(...) { ... }
int sum(int x, int y) {
int ret = 0;
for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
for (int j = y; j >= 0; j = (j & (j + 1)) - 1)
ret += bit[i][j];
return ret;
}
void add(int x, int y, int delta) {
for (int i = x; i < n; i = i | (i + 1))
for (int j = y; j < m; j = j | (j + 1))
bit[i][j] += delta;
}
};
رویکرد اندیسگذاری از یک¶
برای این رویکرد، ما نیازمندیها و تعریف $T[]$ و $g()$ را کمی تغییر میدهیم. ما میخواهیم $T[i]$ مجموع بازه $[g(i)+1, i]$ را ذخیره کند. این موضوع پیادهسازی را کمی تغییر میدهد و امکان تعریف مشابه و زیبایی را برای $g(i)$ فراهم میکند:
تابع sum(عدد صحیح r):
نتیجه = 0
تا زمانی که (r > 0):
نتیجه += t[r]
r = g(r)
بازگرداندن نتیجه
تابع increase(عدد صحیح i, عدد صحیح delta):
برای تمام j هایی که g(j) < i <= j:
t[j] += delta
محاسبه $g(i)$ به این صورت تعریف میشود: برعکس کردن (toggle) آخرین بیت ۱ تنظیمشده در نمایش دودویی $i$.
آخرین بیت تنظیمشده را میتوان با استفاده از $i ~\&~ (-i)$ استخراج کرد، بنابراین عملیات را میتوان به این صورت بیان کرد:
و دیدن این نکته دشوار نیست که وقتی میخواهید $A[j]$ را بهروزرسانی کنید، باید تمام مقادیر $T[j]$ را در دنباله $i,~ h(i),~ h(h(i)),~ \dots$ تغییر دهید، که در آن $h(i)$ به صورت زیر تعریف میشود:
همانطور که میبینید، مزیت اصلی این رویکرد این است که عملیات بیتی به خوبی یکدیگر را تکمیل میکنند.
پیادهسازی زیر را میتوان مانند سایر پیادهسازیها استفاده کرد، اما در داخل از اندیسگذاری از یک استفاده میکند.
struct FenwickTreeOneBasedIndexing {
vector<int> bit; // درخت اندیسگذاری شده دودویی
int n;
FenwickTreeOneBasedIndexing(int n) {
this->n = n + 1;
bit.assign(n + 1, 0);
}
FenwickTreeOneBasedIndexing(vector<int> a)
: FenwickTreeOneBasedIndexing(a.size()) {
for (size_t i = 0; i < a.size(); i++)
add(i, a[i]);
}
int sum(int idx) {
int ret = 0;
for (++idx; idx > 0; idx -= idx & -idx)
ret += bit[idx];
return ret;
}
int sum(int l, int r) {
return sum(r) - sum(l - 1);
}
void add(int idx, int delta) {
for (++idx; idx < n; idx += idx & -idx)
bit[idx] += delta;
}
};
عملیات روی بازهها¶
یک درخت فنویک میتواند از عملیات بازهای زیر پشتیبانی کند:
- بهروزرسانی نقطهای و پرسوجوی بازهای
- بهروزرسانی بازهای و پرسوجوی نقطهای
- بهروزرسانی بازهای و پرسوجوی بازهای
۱. بهروزرسانی نقطهای و پرسوجوی بازهای¶
این همان درخت فنویک معمولی است که در بالا توضیح داده شد.
۲. بهروزرسانی بازهای و پرسوجوی نقطهای¶
با استفاده از ترفندهای ساده، میتوانیم عملیات معکوس را نیز انجام دهیم: افزایش بازهها و پرسوجو برای مقادیر تکی.
فرض کنید درخت فنویک با صفرها مقداردهی اولیه شده است.
فرض کنید میخواهیم بازه $[l, r]$ را به اندازه $x$ افزایش دهیم.
ما دو عملیات بهروزرسانی نقطهای روی درخت فنویک انجام میدهیم که عبارتند از add(l, x) و add(r+1, -x).
اگر بخواهیم مقدار $A[i]$ را به دست آوریم، کافی است با استفاده از متد معمولی مجموع بازهای، مجموع پیشوندی را بگیریم. برای اینکه ببینیم چرا این درست است، میتوانیم دوباره روی عملیات افزایش قبلی تمرکز کنیم. اگر $i < l$ باشد، دو عملیات بهروزرسانی تأثیری بر پرسوجو ندارند و مجموع ۰ را به دست میآوریم. اگر $i \in [l, r]$ باشد، به دلیل اولین عملیات بهروزرسانی، پاسخ $x$ را میگیریم. و اگر $i > r$ باشد، دومین عملیات بهروزرسانی اثر اولین عملیات را خنثی میکند.
پیادهسازی زیر از اندیسگذاری از یک استفاده میکند.
void add(int idx, int val) {
for (++idx; idx < n; idx += idx & -idx)
bit[idx] += val;
}
void range_add(int l, int r, int val) {
add(l, val);
add(r + 1, -val);
}
int point_query(int idx) {
int ret = 0;
for (++idx; idx > 0; idx -= idx & -idx)
ret += bit[idx];
return ret;
}
توجه: البته افزایش یک نقطه تکی $A[i]$ نیز با range_add(i, i, val) امکانپذیر است.
۳. بهروزرسانی بازهای و پرسوجوی بازهای¶
برای پشتیبانی از هر دو نوع بهروزرسانی بازهای و پرسوجوی بازهای، از دو BIT به نامهای $B_1[]$ و $B_2[]$ که با صفر مقداردهی اولیه شدهاند، استفاده خواهیم کرد.
فرض کنید میخواهیم بازه $[l, r]$ را به اندازه مقدار $x$ افزایش دهیم.
مشابه روش قبلی، دو بهروزرسانی نقطهای روی $B_1$ انجام میدهیم: add(B1, l, x) و add(B1, r+1, -x).
و همچنین $B_2$ را نیز بهروزرسانی میکنیم. جزئیات بعداً توضیح داده خواهد شد.
def range_add(l, r, x):
add(B1, l, x)
add(B1, r+1, -x)
add(B2, l, x*(l-1))
add(B2, r+1, -x*r))
پس از بهروزرسانی بازه $(l, r, x)$، پرسوجوی مجموع بازهای باید مقادیر زیر را برگرداند:
میتوانیم مجموع بازه را به صورت تفاضل دو عبارت بنویسیم، که در آن از $B_1$ برای عبارت اول و از $B_2$ برای عبارت دوم استفاده میکنیم. تفاضل این پرسوجوها، مجموع پیشوندی روی بازه $[0, i]$ را به ما میدهد.
عبارت آخر دقیقاً برابر با عبارات مورد نیاز است. بنابراین میتوانیم از $B_2$ برای حذف جملات اضافی هنگام ضرب $B_1[i]\times i$ استفاده کنیم.
ما میتوانیم با محاسبه مجموعهای پیشوندی برای $l-1$ و $r$ و گرفتن تفاضل آنها، مجموع بازههای دلخواه را پیدا کنیم.
def add(b, idx, x):
while idx <= N:
b[idx] += x
idx += idx & -idx
def range_add(l,r,x):
add(B1, l, x)
add(B1, r+1, -x)
add(B2, l, x*(l-1))
add(B2, r+1, -x*r)
def sum(b, idx):
total = 0
while idx > 0:
total += b[idx]
idx -= idx & -idx
return total
def prefix_sum(idx):
return sum(B1, idx)*idx - sum(B2, idx)
def range_sum(l, r):
return prefix_sum(r) - prefix_sum(l-1)
مسائل تمرینی¶
- UVA 12086 - Potentiometers
- LOJ 1112 - Curious Robin Hood
- LOJ 1266 - Points in Rectangle
- Codechef - SPREAD
- SPOJ - CTRICK
- SPOJ - MATSUM
- SPOJ - DQUERY
- SPOJ - NKTEAM
- SPOJ - YODANESS
- SRM 310 - FloatingMedian
- SPOJ - Ada and Behives
- Hackerearth - Counting in Byteland
- DevSkill - Shan and String (archived)
- Codeforces - Little Artem and Time Machine
- Codeforces - Hanoi Factory
- SPOJ - Tulip and Numbers
- SPOJ - SUMSUM
- SPOJ - Sabir and Gifts
- SPOJ - The Permutation Game Again
- SPOJ - Zig when you Zag
- SPOJ - Cryon
- SPOJ - Weird Points
- SPOJ - Its a Murder
- SPOJ - Bored of Suffixes and Prefixes
- SPOJ - Mega Inversions
- Codeforces - Subsequences
- Codeforces - Ball
- GYM - The Kamphaeng Phet's Chedis
- Codeforces - Garlands
- Codeforces - Inversions after Shuffle
- GYM - Cairo Market
- Codeforces - Goodbye Souvenir
- SPOJ - Ada and Species
- Codeforces - Thor
- CSES - Forest Queries II
- Latin American Regionals 2017 - Fundraising