جستجوی یک جفت پارهخط متقاطع¶
با داشتن $n$ پارهخط در صفحه، باید بررسی کنیم که آیا حداقل دو تا از آنها با یکدیگر تقاطع دارند یا خیر. اگر پاسخ مثبت بود، این جفت پارهخط متقاطع را چاپ کنید؛ انتخاب هر یک از آنها در میان چندین پاسخ ممکن کافی است.
الگوریتم راهحل ساده این است که روی تمام جفتهای پارهخط در $O(n^2)$ پیمایش کرده و برای هر جفت بررسی کنیم که آیا تقاطع دارند یا نه. این مقاله الگوریتمی با زمان اجرای $O(n \log n)$ را توصیف میکند که بر اساس الگوریتم خط جاروب (sweep line) است.
الگوریتم¶
بیایید یک خط عمودی $x = -\infty$ را به صورت ذهنی ترسیم کرده و شروع به حرکت این خط به سمت راست کنیم. در طول حرکت، این خط با پارهخطها برخورد خواهد کرد و هر بار که یک پارهخط با خط ما تقاطع پیدا کند، دقیقاً در یک نقطه تقاطع خواهد داشت (فرض میکنیم که هیچ پارهخط عمودی وجود ندارد).
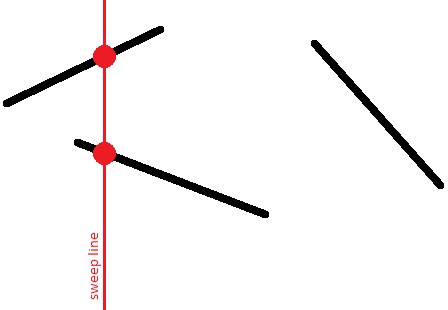
بنابراین، برای هر پارهخط، در یک نقطه زمانی، نقطهی آن روی خط جاروب ظاهر میشود، سپس با حرکت خط، این نقطه جابجا شده و در نهایت، در نقطهای دیگر، پارهخط از خط جاروب ناپدید میشود.
ما به ترتیب نسبی پارهخطها در راستای عمودی علاقهمندیم. بهطور مشخص، ما لیستی از پارهخطهایی که در یک زمان معین خط جاروب را قطع میکنند، ذخیره خواهیم کرد که در آن پارهخطها بر اساس مختصات $y$ خود روی خط جاروب مرتب شدهاند.
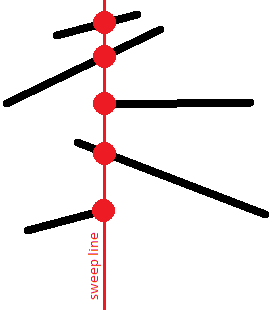
این ترتیب از آن جهت جالب است که پارهخطهای متقاطع حداقل در یک لحظه مختصات $y$ یکسانی خواهند داشت:
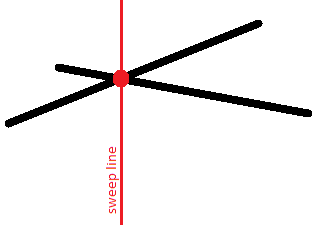
گزارههای کلیدی را فرمولبندی میکنیم:
- برای یافتن یک جفت متقاطع، کافی است در هر موقعیت ثابت خط جاروب، فقط پارهخطهای مجاور را در نظر بگیریم.
- کافی است خط جاروب را نه در تمام موقعیتهای حقیقی ممکن $(-\infty \ldots +\infty)$، بلکه فقط در موقعیتهایی که پارهخطهای جدید ظاهر یا پارهخطهای قدیمی ناپدید میشوند، در نظر بگیریم. به عبارت دیگر، کافی است خود را فقط به موقعیتهای برابر با طول (مختصات x) نقاط انتهایی پارهخطها محدود کنیم.
- هنگامی که یک پارهخط جدید ظاهر میشود، کافی است آن را در مکان مورد نظر در لیستی که برای خط جاروب قبلی به دست آمده، درج کنیم. ما فقط باید تقاطع پارهخط اضافهشده با همسایههای فوری آن در لیست (بالایی و پایینی) را بررسی کنیم.
- اگر پارهخطی ناپدید شود، کافی است آن را از لیست فعلی حذف کنیم. پس از آن، لازم است تقاطع همسایههای بالایی و پایینی در لیست را بررسی کنیم.
- تغییرات دیگری در ترتیب پارهخطها در لیست، به جز موارد توصیف شده، وجود ندارد. هیچ بررسی تقاطع دیگری لازم نیست.
برای درک درستی این گزارهها، نکات زیر کافی است:
- دو پارهخط غیرمتقاطع هرگز ترتیب نسبی خود را تغییر نمیدهند.
در واقع، اگر یک پارهخط ابتدا بالاتر از دیگری بوده و سپس پایینتر از آن قرار گیرد، پس بین این دو لحظه، تقاطعی بین این دو پارهخط رخ داده است. - دو پارهخط غیرمتقاطع همچنین نمیتوانند مختصات $y$ یکسانی داشته باشند.
- از این نتیجه میگیریم که در لحظه ظاهر شدن پارهخط میتوانیم موقعیت آن را در صف پیدا کنیم و دیگر نیازی به جابجایی این پارهخط در صف نخواهیم داشت: ترتیب آن نسبت به سایر پارهخطها در صف تغییر نخواهد کرد.
- دو پارهخط متقاطع در لحظه رسیدن به نقطه تقاطعشان، در صف همسایه یکدیگر خواهند بود.
- بنابراین، برای یافتن جفتهای پارهخط متقاطع، کافی است تقاطع تمام و فقط آن جفت پارهخطهایی را بررسی کنیم که در طول حرکت خط جاروب حداقل یک بار با یکدیگر همسایه بودهاند.
به راحتی میتوان دریافت که کافی است فقط پارهخط اضافهشده را با همسایههای بالایی و پایینی آن بررسی کنیم، و همچنین هنگام حذف یک پارهخط — همسایههای بالایی و پایینی آن را (که پس از حذف، همسایه یکدیگر خواهند شد) بررسی کنیم. - باید توجه داشت که در یک موقعیت ثابت خط جاروب، ما باید ابتدا تمام پارهخطهایی را که در این مختصات x شروع میشوند، اضافه کنیم و سپس تمام پارهخطهایی را که در اینجا به پایان میرسند، حذف کنیم.
بنابراین، ما تقاطع پارهخطها روی رأس را از دست نمیدهیم: یعنی مواردی که دو پارهخط یک رأس مشترک دارند. - توجه داشته باشید که پارهخطهای عمودی در واقع بر صحت الگوریتم تأثیر نمیگذارند.
این پارهخطها با این واقعیت متمایز میشوند که در یک زمان ظاهر و ناپدید میشوند. با این حال، با توجه به نکته قبلی، میدانیم که همه پارهخطها ابتدا به صف اضافه میشوند و سپس حذف خواهند شد. بنابراین، اگر پارهخط عمودی با پارهخط دیگری که در آن لحظه باز است (از جمله یک پارهخط عمودی دیگر) تقاطع داشته باشد، این تقاطع شناسایی خواهد شد.
پارهخطهای عمودی را در کجای صف قرار دهیم؟ به هر حال، یک پارهخط عمودی یک مختصات $y$ مشخص ندارد، بلکه در تمام طول یک پارهخط در امتداد محور $y$ کشیده شده است. با این حال، به راحتی میتوان فهمید که هر مختصاتی از این پارهخط را میتوان به عنوان مختصات $y$ در نظر گرفت.
بنابراین، کل الگوریتم حداکثر $2n$ بار تست تقاطع یک جفت پارهخط را انجام میدهد و $O(n)$ عملیات با صف پارهخطها انجام خواهد داد (عملیات $O(1)$ در زمان ظهور و ناپدید شدن هر پارهخط).
بنابراین، رفتار مجانبی نهایی الگوریتم $O(n \log n)$ است.
پیادهسازی¶
پیادهسازی کامل الگوریتم توصیفشده را ارائه میدهیم:
const double EPS = 1E-9;
struct pt {
double x, y;
};
struct seg {
pt p, q;
int id;
double get_y(double x) const {
if (abs(p.x - q.x) < EPS)
return p.y;
return p.y + (q.y - p.y) * (x - p.x) / (q.x - p.x);
}
};
bool intersect1d(double l1, double r1, double l2, double r2) {
if (l1 > r1)
swap(l1, r1);
if (l2 > r2)
swap(l2, r2);
return max(l1, l2) <= min(r1, r2) + EPS;
}
int vec(const pt& a, const pt& b, const pt& c) {
double s = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
return abs(s) < EPS ? 0 : s > 0 ? +1 : -1;
}
bool intersect(const seg& a, const seg& b)
{
return intersect1d(a.p.x, a.q.x, b.p.x, b.q.x) &&
intersect1d(a.p.y, a.q.y, b.p.y, b.q.y) &&
vec(a.p, a.q, b.p) * vec(a.p, a.q, b.q) <= 0 &&
vec(b.p, b.q, a.p) * vec(b.p, b.q, a.q) <= 0;
}
bool operator<(const seg& a, const seg& b)
{
double x = max(min(a.p.x, a.q.x), min(b.p.x, b.q.x));
return a.get_y(x) < b.get_y(x) - EPS;
}
struct event {
double x;
int tp, id;
event() {}
event(double x, int tp, int id) : x(x), tp(tp), id(id) {}
bool operator<(const event& e) const {
if (abs(x - e.x) > EPS)
return x < e.x;
return tp > e.tp;
}
};
set<seg> s;
vector<set<seg>::iterator> where;
set<seg>::iterator prev(set<seg>::iterator it) {
return it == s.begin() ? s.end() : --it;
}
set<seg>::iterator next(set<seg>::iterator it) {
return ++it;
}
pair<int, int> solve(const vector<seg>& a) {
int n = (int)a.size();
vector<event> e;
for (int i = 0; i < n; ++i) {
e.push_back(event(min(a[i].p.x, a[i].q.x), +1, i));
e.push_back(event(max(a[i].p.x, a[i].q.x), -1, i));
}
sort(e.begin(), e.end());
s.clear();
where.resize(a.size());
for (size_t i = 0; i < e.size(); ++i) {
int id = e[i].id;
if (e[i].tp == +1) {
set<seg>::iterator nxt = s.lower_bound(a[id]), prv = prev(nxt);
if (nxt != s.end() && intersect(*nxt, a[id]))
return make_pair(nxt->id, id);
if (prv != s.end() && intersect(*prv, a[id]))
return make_pair(prv->id, id);
where[id] = s.insert(nxt, a[id]);
} else {
set<seg>::iterator nxt = next(where[id]), prv = prev(where[id]);
if (nxt != s.end() && prv != s.end() && intersect(*nxt, *prv))
return make_pair(prv->id, nxt->id);
s.erase(where[id]);
}
}
return make_pair(-1, -1);
}
تابع اصلی در اینجا solve() است که در صورت وجود، پارهخطهای متقاطع را برمیگرداند، یا در صورت عدم وجود تقاطع، (-1, -1) را برمیگرداند.
بررسی تقاطع دو پارهخط توسط تابع intersect() انجام میشود که از الگوریتمی مبتنی بر مساحت جهتدار مثلث استفاده میکند.
صف پارهخطها متغیر سراسری s است که یک set<seg> میباشد. iteratorهایی که موقعیت هر پارهخط را در صف مشخص میکنند (برای حذف راحت پارهخطها از صف)، در آرایه سراسری where ذخیره میشوند.
دو تابع کمکی prev() و next() نیز معرفی شدهاند که iteratorهایی به عناصر قبلی و بعدی را برمیگردانند (یا end()، اگر چنین عنصری وجود نداشته باشد).
ثابت EPS خطای مقایسه دو عدد حقیقی را نشان میدهد (عمدتاً هنگام بررسی تقاطع دو پارهخط استفاده میشود).