جمع مینکوفسکی برای چندضلعیهای محدب¶
تعریف¶
دو مجموعه نقطه $A$ و $B$ را روی یک صفحه در نظر بگیرید. جمع مینکوفسکی $A + B$ به صورت $\{a + b| a \in A, b \in B\}$ تعریف میشود. در اینجا، حالتی را بررسی میکنیم که $A$ و $B$ از چندضلعیهای محدب $P$ و $Q$ به همراه فضای داخلیشان تشکیل شده باشند. در سراسر این مقاله، چندضلعیها را با دنبالهای مرتب از رئوسشان مشخص میکنیم، به طوری که نمادهایی مانند $|P|$ یا $P_i$ معنا پیدا کنند. مشخص شده است که حاصلجمع دو چندضلعی محدب $P$ و $Q$، یک چندضلعی محدب با حداکثر $|P| + |Q|$ رأس است.
الگوریتم¶
در اینجا، چندضلعیها را به صورت چرخشی شمارهگذاری میکنیم، یعنی $P_{|P|} = P_0$، $Q_{|Q|} = Q_0$ و غیره.
از آنجایی که اندازه حاصلجمع از نظر اندازه چندضلعیهای اولیه خطی است، باید به دنبال الگوریتمی با زمان اجرای خطی باشیم. فرض کنید هر دو چندضلعی در جهت پادساعتگرد مرتب شده باشند. دنباله یالهای $\{\overrightarrow{P_iP_{i+1}}\}$ و $\{\overrightarrow{Q_jQ_{j+1}}\}$ را که بر اساس زاویه قطبی مرتب شدهاند، در نظر بگیرید. ادعا میکنیم که دنباله یالهای $P + Q$ را میتوان با ادغام این دو دنباله، با حفظ ترتیب زاویه قطبی و جایگزین کردن بردارهای همجهت متوالی با حاصلجمعشان، به دست آورد. استفاده مستقیم از این ایده منجر به یک الگوریتم با زمان اجرای خطی میشود، اما بازیابی رئوس $P + Q$ از روی دنباله یالها نیازمند جمع مکرر بردارها است که اگر با مختصات ممیز شناور کار کنیم، ممکن است مشکلات دقت ناخواستهای ایجاد کند. بنابراین، ما یک تغییر جزئی در این ایده را شرح خواهیم داد.
ابتدا باید رئوس را به گونهای مرتب کنیم که اولین رأس هر چندضلعی دارای کمترین مختص y باشد (در صورت وجود چندین رأس با این ویژگی، رأسی را انتخاب کنید که کمترین مختص x را دارد). پس از این کار، یالهای هر دو چندضلعی بر اساس زاویه قطبی مرتب میشوند، بنابراین نیازی به مرتبسازی دستی آنها نیست. اکنون دو اشارهگر $i$ (که به یک رأس از $P$ اشاره میکند) و $j$ (که به یک رأس از $Q$ اشاره میکند) ایجاد میکنیم که هر دو در ابتدا روی 0 تنظیم شدهاند. مراحل زیر را تا زمانی که $i < |P|$ یا $j < |Q|$ باشد تکرار میکنیم.
-
$P_i + Q_j$ را به $P + Q$ اضافه کنید.
-
زاویههای قطبی $\overrightarrow{P_iP_{i + 1}}$ و $\overrightarrow{Q_jQ_{j+1}}$ را مقایسه کنید.
-
اشارهگری را که به زاویه کوچکتر تعلق دارد افزایش دهید (اگر زاویهها مساوی بودند، هر دو را افزایش دهید).
تصویرسازی¶
در اینجا یک تصویرسازی جالب وجود دارد که ممکن است به شما در درک بهتر موضوع کمک کند.
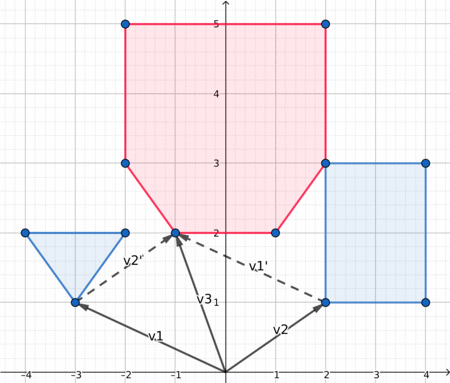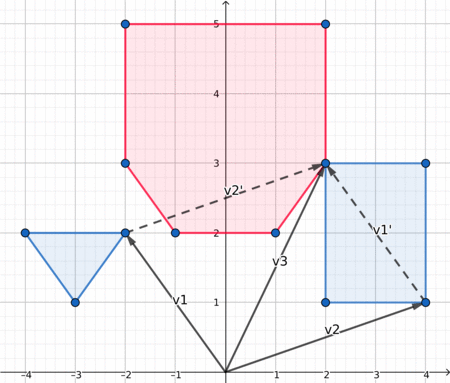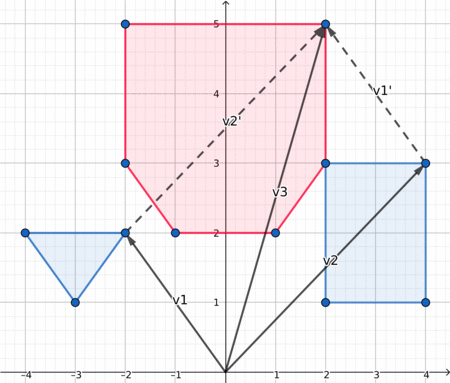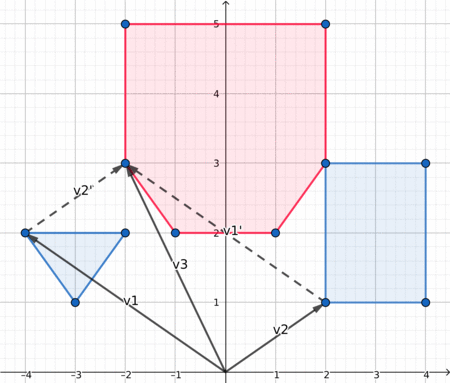
فاصله بین دو چندضلعی¶
یکی از رایجترین کاربردهای جمع مینکوفسکی، محاسبه فاصله بین دو چندضلعی محدب (یا به سادگی، بررسی تقاطع آنها) است. فاصله بین دو چندضلعی محدب $P$ و $Q$ به صورت $\min\limits_{a \in P, b \in Q} ||a - b||$ تعریف میشود. میتوان توجه داشت که این فاصله همیشه بین دو رأس یا یک رأس و یک یال به دست میآید، بنابراین میتوانیم به راحتی فاصله را با پیچیدگی زمانی $O(|P||Q|)$ پیدا کنیم. با این حال، با استفاده هوشمندانه از جمع مینکوفسکی میتوانیم این پیچیدگی را به $O(|P| + |Q|)$ کاهش دهیم.
اگر $Q$ را نسبت به نقطه $(0, 0)$ قرینه کنیم و چندضلعی $-Q$ را به دست آوریم، مسئله به یافتن کوتاهترین فاصله بین یک نقطه در $P + (-Q)$ و نقطه $(0, 0)$ خلاصه میشود. میتوانیم این فاصله را در زمان خطی با استفاده از ایده زیر پیدا کنیم. اگر نقطه $(0, 0)$ داخل یا روی مرز چندضلعی باشد، فاصله $0$ است؛ در غیر این صورت، فاصله بین $(0, 0)$ و یکی از رئوس یا یالهای چندضلعی به دست میآید. از آنجایی که جمع مینکوفسکی را میتوان در زمان خطی محاسبه کرد، یک الگوریتم با زمان خطی برای یافتن فاصله بین دو چندضلعی محدب به دست میآوریم.
پیادهسازی¶
در زیر، پیادهسازی جمع مینکوفسکی برای چندضلعیهایی با نقاط صحیح آورده شده است. توجه داشته باشید که در این حالت تمام محاسبات را میتوان با اعداد صحیح انجام داد، زیرا به جای محاسبه زوایای قطبی و مقایسه مستقیم آنها، میتوانیم به علامت ضرب خارجی دو بردار نگاه کنیم.
struct pt{
long long x, y;
pt operator + (const pt & p) const {
return pt{x + p.x, y + p.y};
}
pt operator - (const pt & p) const {
return pt{x - p.x, y - p.y};
}
long long cross(const pt & p) const {
return x * p.y - y * p.x;
}
};
void reorder_polygon(vector<pt> & P){
size_t pos = 0;
for(size_t i = 1; i < P.size(); i++){
if(P[i].y < P[pos].y || (P[i].y == P[pos].y && P[i].x < P[pos].x))
pos = i;
}
rotate(P.begin(), P.begin() + pos, P.end());
}
vector<pt> minkowski(vector<pt> P, vector<pt> Q){
// اولین رأس باید پایینترین رأس باشد
reorder_polygon(P);
reorder_polygon(Q);
// باید از اندیسگذاری چرخشی اطمینان حاصل کنیم
P.push_back(P[0]);
P.push_back(P[1]);
Q.push_back(Q[0]);
Q.push_back(Q[1]);
// بخش اصلی
vector<pt> result;
size_t i = 0, j = 0;
while(i < P.size() - 2 || j < Q.size() - 2){
result.push_back(P[i] + Q[j]);
auto cross = (P[i + 1] - P[i]).cross(Q[j + 1] - Q[j]);
if(cross >= 0 && i < P.size() - 2)
++i;
if(cross <= 0 && j < Q.size() - 2)
++j;
}
return result;
}