غربال اراتوستن¶
غربال اراتوستن الگوریتمی برای یافتن تمام اعداد اول در بازهی $[1;n]$ با $O(n \log \log n)$ عملیات است.
الگوریتم بسیار ساده است: در ابتدا تمام اعداد بین 2 تا $n$ را مینویسیم. تمام مضربهای سرهی 2 را (چون 2 کوچکترین عدد اول است) به عنوان مرکب علامت میزنیم. مضرب سرهی یک عدد $x$ عددی بزرگتر از $x$ و بخشپذیر بر $x$ است. سپس عدد بعدی را که به عنوان مرکب علامت نخورده است پیدا میکنیم، که در این مورد 3 است. این یعنی 3 اول است، و ما تمام مضربهای سرهی 3 را به عنوان مرکب علامت میزنیم. عدد بعدی علامت نخورده 5 است، که عدد اول بعدی است، و ما تمام مضربهای سرهی آن را علامت میزنیم. و این روند را تا زمانی که تمام اعداد در این ردیف را پردازش کنیم ادامه میدهیم.
در تصویر زیر میتوانید یک نمایش تصویری از الگوریتم برای محاسبهی تمام اعداد اول در بازهی $[1; 16]$ را ببینید. میتوان دید که خیلی وقتها اعداد را چندین بار به عنوان مرکب علامت میزنیم.
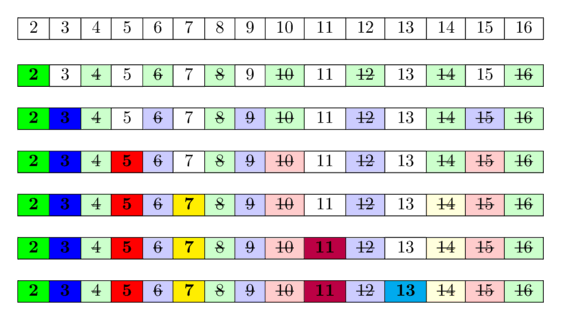
ایدهی پشت این الگوریتم این است: یک عدد اول است، اگر هیچیک از اعداد اول کوچکتر از آن بر آن بخشپذیر نباشد. از آنجایی که ما اعداد اول را به ترتیب پیمایش میکنیم، از قبل تمام اعدادی را که بر حداقل یکی از اعداد اول بخشپذیر هستند، به عنوان مرکب علامت زدهایم. بنابراین اگر به خانهای برسیم و علامت نخورده باشد، آنگاه بر هیچ عدد اول کوچکتری بخشپذیر نیست و در نتیجه باید اول باشد.
پیادهسازی¶
int n;
vector<bool> is_prime(n+1, true);
is_prime[0] = is_prime[1] = false;
for (int i = 2; i <= n; i++) {
if (is_prime[i] && (long long)i * i <= n) {
for (int j = i * i; j <= n; j += i)
is_prime[j] = false;
}
}
این کد ابتدا تمام اعداد به جز صفر و یک را به عنوان اعداد اول بالقوه علامتگذاری میکند، سپس فرآیند غربال کردن اعداد مرکب را آغاز میکند.
برای این کار، روی تمام اعداد از $2$ تا $n$ پیمایش میکند.
اگر عدد فعلی $i$ یک عدد اول باشد، تمام اعدادی را که مضرب $i$ هستند، از $i^2$ شروع کرده و به عنوان اعداد مرکب علامت میزند.
این خود یک بهینهسازی نسبت به روش سادهی پیادهسازی است و مجاز است زیرا تمام اعداد کوچکتر که مضرب $i$ هستند، لزوماً یک عامل اول کوچکتر از $i$ نیز دارند، بنابراین همهی آنها قبلاً غربال شدهاند.
از آنجایی که $i^2$ به راحتی میتواند از نوع int سرریز (overflow) کند، بررسی اضافی با استفاده از نوع long long قبل از حلقهی تو در توی دوم انجام میشود.
با چنین پیادهسازی، الگوریتم (بدیهتاً) $O(n)$ حافظه مصرف میکند و $O(n \log \log n)$ عملیات انجام میدهد (بخش بعدی را ببینید).
تحلیل مجانبی¶
اثبات زمان اجرای $O(n \log n)$ بدون دانستن چیزی در مورد توزیع اعداد اول ساده است - با نادیده گرفتن بررسی is_prime، حلقهی داخلی (حداکثر) $n/i$ بار برای $i = 2, 3, 4, \dots$ اجرا میشود، که منجر به این میشود که تعداد کل عملیات در حلقهی داخلی یک سری هارمونیک مانند $n(1/2 + 1/3 + 1/4 + \cdots)$ باشد که توسط $O(n \log n)$ کراندار میشود.
بیایید ثابت کنیم که زمان اجرای الگوریتم $O(n \log \log n)$ است. الگوریتم برای هر عدد اول $p \le n$ در حلقهی داخلی، $\frac{n}{p}$ عملیات انجام میدهد. بنابراین، باید عبارت زیر را ارزیابی کنیم:
بیایید دو واقعیت شناخته شده را یادآوری کنیم.
- تعداد اعداد اول کوچکتر یا مساوی $n$ تقریباً $\frac n {\ln n}$ است.
- $k$-امین عدد اول تقریباً برابر با $k \ln k$ است (این از واقعیت قبلی نتیجه میشود).
بنابراین میتوانیم مجموع را به صورت زیر بنویسیم:
در اینجا اولین عدد اول یعنی 2 را از مجموع جدا کردیم، زیرا $k = 1$ در تقریب $k \ln k$ برابر 0 است و باعث تقسیم بر صفر میشود.
حال، بیایید این مجموع را با استفاده از انتگرال همان تابع بر روی $k$ از $2$ تا $\frac n {\ln n}$ ارزیابی کنیم (میتوانیم چنین تقریبی بزنیم زیرا در واقع، این مجموع به عنوان تقریب انتگرال با استفاده از روش مستطیلها با آن مرتبط است):
پادمشتق انتگرالده برابر با $\ln \ln k$ است. با استفاده از یک جایگذاری و حذف جملات با مرتبهی پایینتر، به نتیجهی زیر میرسیم:
حال، با بازگشت به مجموع اصلی، ارزیابی تقریبی آن را به دست میآوریم:
میتوانید اثبات دقیقتری (که ارزیابی دقیقتری با دقت در حد ضریب ثابت ارائه میدهد) را در کتاب "An Introduction to the Theory of Numbers" نوشتهی Hardy & Wright (صفحه 349) پیدا کنید.
بهینهسازیهای مختلف غربال اراتوستن¶
بزرگترین ضعف الگوریتم این است که چندین بار در حافظه "قدم میزند" و فقط عناصر تکی را دستکاری میکند. این رفتار با حافظهی نهان (cache) سازگار نیست. به همین دلیل، ثابت پنهان در $O(n \log \log n)$ نسبتاً بزرگ است.
علاوه بر این، حافظهی مصرفی برای مقادیر بزرگ $n$ یک گلوگاه (bottleneck) است.
روشهای ارائه شده در زیر به ما اجازه میدهند تا تعداد عملیات انجام شده را کاهش دهیم و همچنین حافظهی مصرفی را به طور قابل توجهی کوتاه کنیم.
غربال کردن تا ریشه¶
بدیهی است که برای یافتن تمام اعداد اول تا $n$، کافی است که غربال کردن را فقط با اعداد اولی انجام دهیم که از ریشهی دوم $n$ تجاوز نمیکنند.
int n;
vector<bool> is_prime(n+1, true);
is_prime[0] = is_prime[1] = false;
for (int i = 2; i * i <= n; i++) {
if (is_prime[i]) {
for (int j = i * i; j <= n; j += i)
is_prime[j] = false;
}
}
چنین بهینهسازی بر روی پیچیدگی تأثیری ندارد (در واقع، با تکرار اثبات ارائه شده در بالا، به ارزیابی $n \ln \ln \sqrt n + o(n)$ میرسیم، که طبق خواص لگاریتمها از نظر مجانبی یکسان است)، هرچند تعداد عملیات به طور قابل توجهی کاهش مییابد.
غربال کردن فقط با اعداد فرد¶
از آنجایی که تمام اعداد زوج (به جز 2) مرکب هستند، میتوانیم بررسی اعداد زوج را به کلی متوقف کنیم. به جای آن، فقط باید با اعداد فرد کار کنیم.
اولاً، این کار به ما اجازه میدهد تا حافظهی مورد نیاز را نصف کنیم. ثانیاً، تعداد عملیات انجام شده توسط الگوریتم را تقریباً به نصف کاهش میدهد.
مصرف حافظه و سرعت عملیات¶
باید توجه داشت که این دو پیادهسازی از غربال اراتوستن با استفاده از ساختار دادهی vector<bool>، $n$ بیت حافظه مصرف میکنند.
vector<bool> یک کانتینر معمولی نیست که یک سری از bool ها را ذخیره کند (چرا که در اکثر معماریهای کامپیوتری یک bool یک بایت از حافظه را اشغال میکند). این یک تخصص بهینهسازی حافظه از vector<T> است که تنها $\frac{N}{8}$ بایت حافظه مصرف میکند.
معماریهای پردازندههای مدرن با بایتها بسیار کارآمدتر از بیتها کار میکنند، زیرا معمولاً نمیتوانند مستقیماً به بیتها دسترسی داشته باشند. بنابراین در زیرساخت vector<bool>، بیتها در یک حافظهی پیوستهی بزرگ ذخیره میشوند، دسترسی به حافظه در بلوکهای چند بایتی انجام میشود، و بیتها با عملیات بیتی مانند bit masking و bit shifting استخراج/تنظیم میشوند.
به همین دلیل، هنگام خواندن یا نوشتن بیتها با vector<bool>، مقداری سربار (overhead) وجود دارد، و خیلی وقتها استفاده از vector<char> (که برای هر ورودی ۱ بایت استفاده میکند، یعنی ۸ برابر حافظه) سریعتر است.
با این حال، برای پیادهسازیهای سادهی غربال اراتوستن، استفاده از vector<bool> سریعتر است. شما به سرعت بارگذاری دادهها در حافظهی نهان (cache) محدود هستید، و بنابراین استفاده از حافظهی کمتر مزیت بزرگی به حساب میآید. یک بنچمارک (لینک) نشان میدهد که استفاده از vector<bool> بین 1.4 تا 1.7 برابر سریعتر از vector<char> است.
همین ملاحظات برای bitset نیز صادق است. این نیز یک روش کارآمد برای ذخیرهسازی بیتها، مشابه vector<bool> است، بنابراین تنها $\frac{N}{8}$ بایت حافظه میگیرد، اما در دسترسی به عناصر کمی کندتر است. در بنچمارک بالا، عملکرد bitset کمی بدتر از vector<bool> است. یک اشکال دیگر bitset این است که باید اندازه را در زمان کامپایل بدانید.
غربال قطعهبندی شده¶
از بهینهسازی "غربال کردن تا ریشه" نتیجه میشود که نیازی به نگهداری کل آرایهی is_prime[1...n] در تمام زمانها نیست. برای غربال کردن کافی است فقط اعداد اول تا ریشهی $n$، یعنی prime[1... sqrt(n)] را نگه داریم، کل بازه را به بلوکهایی تقسیم کنیم و هر بلوک را به طور جداگانه غربال کنیم.
فرض کنید $s$ یک ثابت باشد که اندازهی بلوک را تعیین میکند، آنگاه در مجموع $\lceil {\frac n s} \rceil$ بلوک داریم، و بلوک $k$ ($k = 0 ... \lfloor {\frac n s} \rfloor$) شامل اعداد در بازهی $[ks; ks + s - 1]$ است. ما میتوانیم به نوبت روی بلوکها کار کنیم، یعنی برای هر بلوک $k$، تمام اعداد اول (از $1$ تا $\sqrt n$) را پیمایش کرده و با استفاده از آنها غربال را انجام میدهیم. شایان ذکر است که هنگام کار با اعداد اولیه باید استراتژی را کمی تغییر دهیم: اول اینکه، تمام اعداد اول از بازهی $[1; \sqrt n]$ نباید خودشان را حذف کنند؛ و دوم اینکه، اعداد $0$ و $1$ باید به عنوان اعداد غیر اول علامتگذاری شوند. هنگام کار روی آخرین بلوک، نباید فراموش کرد که آخرین عدد مورد نیاز $n$ لزوماً در انتهای بلوک قرار ندارد.
همانطور که قبلاً بحث شد، پیادهسازی معمول غربال اراتوستن به سرعت بارگذاری دادهها در حافظههای نهان CPU محدود است. با تقسیم بازهی اعداد اول بالقوه $[1; n]$ به بلوکهای کوچکتر، هرگز مجبور نیستیم چندین بلوک را همزمان در حافظه نگه داریم و تمام عملیات بسیار سازگارتر با cache میشوند. از آنجایی که دیگر به سرعت cache محدود نیستیم، میتوانیم vector<bool> را با vector<char> جایگزین کنیم و مقداری عملکرد اضافی به دست آوریم، زیرا پردازندهها میتوانند خواندن و نوشتن با بایتها را مستقیماً انجام دهند و نیازی به تکیه بر عملیات بیتی برای استخراج بیتهای جداگانه ندارند. بنچمارک (لینک) نشان میدهد که استفاده از vector<char> در این شرایط حدود 3 برابر سریعتر از vector<bool> است. یک نکتهی احتیاطی: این اعداد ممکن است بسته به معماری، کامپایلر و سطوح بهینهسازی متفاوت باشند.
در اینجا یک پیادهسازی داریم که تعداد اعداد اول کوچکتر یا مساوی $n$ را با استفاده از غربال بلوکی میشمارد.
int count_primes(int n) {
const int S = 10000;
vector<int> primes;
int nsqrt = sqrt(n);
vector<char> is_prime(nsqrt + 2, true);
for (int i = 2; i <= nsqrt; i++) {
if (is_prime[i]) {
primes.push_back(i);
for (int j = i * i; j <= nsqrt; j += i)
is_prime[j] = false;
}
}
int result = 0;
vector<char> block(S);
for (int k = 0; k * S <= n; k++) {
fill(block.begin(), block.end(), true);
int start = k * S;
for (int p : primes) {
int start_idx = (start + p - 1) / p;
int j = max(start_idx, p) * p - start;
for (; j < S; j += p)
block[j] = false;
}
if (k == 0)
block[0] = block[1] = false;
for (int i = 0; i < S && start + i <= n; i++) {
if (block[i])
result++;
}
}
return result;
}
زمان اجرای غربال بلوکی مانند غربال اراتوستن معمولی است (مگر اینکه اندازهی بلوکها بسیار کوچک باشد)، اما حافظهی مورد نیاز به $O(\sqrt{n} + S)$ کاهش مییابد و نتایج بهتری از نظر حافظهی نهان (caching) داریم. از سوی دیگر، برای هر جفت بلوک و عدد اول از بازهی $[1; \sqrt{n}]$ یک عمل تقسیم وجود خواهد داشت، و این برای اندازههای بلوک کوچکتر بسیار بدتر خواهد بود. بنابراین، لازم است هنگام انتخاب ثابت $S$ تعادل را حفظ کنیم. ما بهترین نتایج را برای اندازههای بلوک بین $10^4$ و $10^5$ به دست آوردیم.
یافتن اعداد اول در یک بازه¶
گاهی اوقات لازم است تمام اعداد اول را در یک بازهی $[L,R]$ با اندازهی کوچک (مثلاً $R - L + 1 \approx 10^7$) پیدا کنیم، در حالی که $R$ میتواند بسیار بزرگ باشد (مثلاً $10^{12}$).
برای حل چنین مسئلهای، میتوانیم از ایدهی غربال قطعهبندی شده استفاده کنیم. ما تمام اعداد اول تا $\sqrt R$ را از پیش تولید میکنیم و از آن اعداد اول برای علامتگذاری تمام اعداد مرکب در بازهی $[L, R]$ استفاده میکنیم.
vector<char> segmentedSieve(long long L, long long R) {
// generate all primes up to sqrt(R)
long long lim = sqrt(R);
vector<char> mark(lim + 1, false);
vector<long long> primes;
for (long long i = 2; i <= lim; ++i) {
if (!mark[i]) {
primes.emplace_back(i);
for (long long j = i * i; j <= lim; j += i)
mark[j] = true;
}
}
vector<char> isPrime(R - L + 1, true);
for (long long i : primes)
for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
isPrime[j - L] = false;
if (L == 1)
isPrime[0] = false;
return isPrime;
}
همچنین ممکن است که تمام اعداد اول را از پیش تولید نکنیم:
vector<char> segmentedSieveNoPreGen(long long L, long long R) {
vector<char> isPrime(R - L + 1, true);
long long lim = sqrt(R);
for (long long i = 2; i <= lim; ++i)
for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
isPrime[j - L] = false;
if (L == 1)
isPrime[0] = false;
return isPrime;
}
بدیهی است که پیچیدگی بدتر است، که برابر با $O((R - L + 1) \log (R) + \sqrt R)$ میباشد. با این حال، در عمل هنوز هم بسیار سریع اجرا میشود.
اصلاح با زمان خطی¶
ما میتوانیم الگوریتم را به گونهای تغییر دهیم که فقط پیچیدگی زمانی خطی داشته باشد. این رویکرد در مقالهی غربال خطی توضیح داده شده است. با این حال، این الگوریتم نیز نقاط ضعف خود را دارد.
مسائل تمرینی¶
- Leetcode - چهار مقسومعلیه
- Leetcode - شمارش اعداد اول
- SPOJ - چاپ تعدادی عدد اول
- SPOJ - حدس پل اردوش
- SPOJ - ترس اولیه
- SPOJ - مثلث اعداد اول (I)
- Codeforces - تقریباً اول
- Codeforces - شرلوک و دوستدخترش
- SPOJ - نامیت در دردسر
- SPOJ - بازینگا!
- Project Euler - اتصال جفتهای اول
- SPOJ - N-عاملی
- SPOJ - دنبالهی باینری اعداد اول
- UVA 11353 - نوعی دیگر از مرتبسازی
- SPOJ - تولیدکنندهی اعداد اول
- SPOJ - چاپ تعدادی عدد اول (سخت)
- Codeforces - مسئلهی نودباخ
- Codeforces - برخورددهندهها