نقاط شبکهای درون چندضلعی غیرشبکهای¶
برای چندضلعیهای شبکهای، فرمول پیک برای شمارش نقاط شبکهای درون چندضلعی وجود دارد. در مورد چندضلعیهایی با رئوس دلخواه چطور؟
بیایید هر یک از یالهای چندضلعی را به صورت جداگانه پردازش کنیم، و پس از آن میتوانیم تعداد نقاط شبکهای زیر هر یال را با در نظر گرفتن جهت آن برای انتخاب علامت، جمع بزنیم (مانند محاسبه مساحت یک چندضلعی با استفاده از ذوزنقهها).
اول از همه باید توجه داشت که اگر یال فعلی دارای نقاط انتهایی $A=(x_1;y_1)$ و $B=(x_2;y_2)$ باشد، میتوان آن را به صورت یک تابع خطی نمایش داد:
حالا یک جایگزینی $x=x'+\lceil x_1 \rceil$ انجام میدهیم تا $b' = b + k \cdot \lceil x_1 \rceil$ شود. این کار به ما اجازه میدهد تا با $x_1'=0$ و $x_2'=x_2 - \lceil x_1 \rceil$ کار کنیم. بیایید $n = \lfloor x_2' \rfloor$ را تعریف کنیم.
برای حفظ یکپارچگی الگوریتم، نقاط روی $x = n$ و روی $y = 0$ را جمع نمیزنیم. این نقاط را میتوان بعداً به صورت دستی اضافه کرد. بنابراین، باید $\sum\limits_{x'=0}^{n - 1} \lfloor k' \cdot x' + b'\rfloor$ را محاسبه کنیم. همچنین فرض میکنیم که $k' \geq 0$ و $b'\geq 0$ است. در غیر این صورت، باید $x'=-t$ را جایگزین کرده و $\lceil|b'|\rceil$ را به $b'$ اضافه کرد.
بیایید بررسی کنیم که چگونه میتوانیم مجموع $\sum\limits_{x=0}^{n - 1} \lfloor k \cdot x + b\rfloor$ را ارزیابی کنیم. دو حالت داریم:
-
$k \geq 1$ یا $b \geq 1$.
در این حالت، باید با جمع زدن نقاط زیر خط $y=\lfloor k \rfloor \cdot x + \lfloor b \rfloor$ شروع کنیم. تعداد این نقاط برابر است با
$$ \sum\limits_{x=0}^{n - 1} \lfloor k \rfloor \cdot x + \lfloor b \rfloor=\dfrac{(\lfloor k \rfloor(n-1)+2\lfloor b \rfloor) n}{2}. $$حالا فقط به نقاط $(x;y)$ علاقهمندیم که در شرط $\lfloor k \rfloor \cdot x + \lfloor b \rfloor < y \leq k\cdot x + b$ صدق کنند. این تعداد با تعداد نقاطی که در شرط $0 < y \leq (k - \lfloor k \rfloor) \cdot x + (b - \lfloor b \rfloor)$ صدق میکنند، یکسان است. بنابراین، مسئله خود را به $k'= k - \lfloor k \rfloor$ و $b' = b - \lfloor b \rfloor$ کاهش دادیم و اکنون هر دو $k'$ و $b'$ کمتر از ۱ هستند. در تصویر زیر، ما نقاط آبی را جمع زده و تابع خطی آبی را از تابع سیاه کم کردهایم تا مسئله را به مقادیر کوچکتری برای $k$ و $b$ کاهش دهیم:
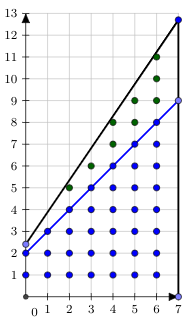
-
$k < 1$ و $b < 1$.
اگر $\lfloor k \cdot n + b\rfloor$ برابر با $0$ باشد، میتوانیم با اطمینان $0$ را برگردانیم. اگر اینطور نباشد، میتوان گفت که هیچ نقطه شبکهای وجود ندارد که در شرط $x < 0$ و $0 < y \leq k \cdot x + b$ صدق کند. این بدان معناست که اگر یک دستگاه مختصات جدید در نظر بگیریم که در آن $O'=(n;\lfloor k\cdot n + b\rfloor)$، محور $x'$ به سمت پایین و محور $y'$ به سمت چپ باشد، به همان پاسخ خواهیم رسید. برای این دستگاه مختصات، ما به نقاط شبکهای در مجموعه زیر علاقهمندیم
$$ \left\{(x;y)~\bigg|~0 \leq x < \lfloor k \cdot n + b\rfloor,~ 0 < y \leq \dfrac{x+(k\cdot n+b)-\lfloor k\cdot n + b \rfloor}{k}\right\} $$که ما را به حالت $k>1$ بازمیگرداند. میتوانید نقطه مرجع جدید $O'$ و محورهای $X'$ و $Y'$ را در تصویر زیر مشاهده کنید:
همانطور که میبینید، در دستگاه مختصات جدید، تابع خطی ضریب $\tfrac 1 k$ خواهد داشت و صفر آن در نقطه $\lfloor k\cdot n + b \rfloor-(k\cdot n+b)$ خواهد بود که فرمول بالا را صحیح میکند.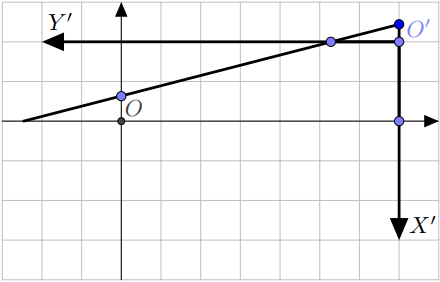
تحلیل پیچیدگی¶
ما باید حداکثر $\dfrac{(k(n-1)+2b)n}{2}$ نقطه را بشماریم. از میان آنها، در همان مرحله اول $\dfrac{\lfloor k \rfloor (n-1)+2\lfloor b \rfloor}{2}$ نقطه را شمارش میکنیم. میتوانیم $b$ را قابل اغماض در نظر بگیریم، زیرا میتوانیم با تبدیل آن به مقداری کمتر از ۱ شروع کنیم. در آن صورت میتوان گفت که ما حدود $\dfrac{\lfloor k \rfloor}{k} \geq \dfrac 1 2$ از کل نقاط را شمارش میکنیم. بنابراین، ما در $O(\log n)$ مرحله کار را به پایان میرسانیم.
پیادهسازی¶
در اینجا یک تابع ساده وجود دارد که تعداد نقاط صحیح $(x;y)$ را برای $0 \leq x < n$ و $0 < y \leq \lfloor k x+b\rfloor$ محاسبه میکند:
int count_lattices(Fraction k, Fraction b, long long n) {
auto fk = k.floor();
auto fb = b.floor();
auto cnt = 0LL;
if (k >= 1 || b >= 1) {
cnt += (fk * (n - 1) + 2 * fb) * n / 2;
k -= fk;
b -= fb;
}
auto t = k * n + b;
auto ft = t.floor();
if (ft >= 1) {
cnt += count_lattices(1 / k, (t - t.floor()) / k, t.floor());
}
return cnt;
}
در اینجا Fraction کلاسی برای کار با اعداد گویا است.
در عمل، اگر قدر مطلق صورت و مخرجها حداکثر $C$ باشد، به نظر میرسد در فراخوانیهای بازگشتی این مقادیر حداکثر $C^2$ خواهند بود، به شرطی که صورت و مخرج را پیوسته بر ب.م.م آنها تقسیم کنید.
با این فرض، میتوان گفت که میتوان از doubleها استفاده کرد و به دقتی برابر با $\varepsilon^2$ نیاز داشت، که در آن $\varepsilon$ دقتی است که $k$ و $b$ با آن داده شدهاند.
این بدان معناست که در تابع جزء صحیح، باید اعدادی را که حداکثر به اندازه $\varepsilon^2$ با یک عدد صحیح اختلاف دارند، به عنوان عدد صحیح در نظر گرفت.