پرش به محتویات

هندسه‌ی پایه

در این مقاله، عملیات پایه‌ای روی نقاط در فضای اقلیدسی را بررسی می‌کنیم که اساس کل هندسه‌ی تحلیلی را تشکیل می‌دهد. برای هر نقطه $\mathbf r$، بردار $\vec{\mathbf r}$ را در نظر می‌گیریم که از $\mathbf 0$ به سمت $\mathbf r$ جهت‌گیری شده است. در ادامه، بین $\mathbf r$ و $\vec{\mathbf r}$ تمایزی قائل نمی‌شویم و از اصطلاح نقطه به عنوان مترادفی برای بردار استفاده می‌کنیم.

عملیات خطی

نقاط دو بعدی و سه بعدی یک فضای خطی را تشکیل می‌دهند، به این معنی که برای آن‌ها جمع نقاط و ضرب یک نقطه در یک عدد تعریف شده است. در ادامه پیاده‌سازی‌های پایه‌ای این عملیات برای نقاط دو بعدی آمده است:

struct point2d {
    ftype x, y;
    point2d() {}
    point2d(ftype x, ftype y): x(x), y(y) {}
    point2d& operator+=(const point2d &t) {
        x += t.x;
        y += t.y;
        return *this;
    }
    point2d& operator-=(const point2d &t) {
        x -= t.x;
        y -= t.y;
        return *this;
    }
    point2d& operator*=(ftype t) {
        x *= t;
        y *= t;
        return *this;
    }
    point2d& operator/=(ftype t) {
        x /= t;
        y /= t;
        return *this;
    }
    point2d operator+(const point2d &t) const {
        return point2d(*this) += t;
    }
    point2d operator-(const point2d &t) const {
        return point2d(*this) -= t;
    }
    point2d operator*(ftype t) const {
        return point2d(*this) *= t;
    }
    point2d operator/(ftype t) const {
        return point2d(*this) /= t;
    }
};
point2d operator*(ftype a, point2d b) {
    return b * a;
}
و برای نقاط سه بعدی: 
struct point3d {
    ftype x, y, z;
    point3d() {}
    point3d(ftype x, ftype y, ftype z): x(x), y(y), z(z) {}
    point3d& operator+=(const point3d &t) {
        x += t.x;
        y += t.y;
        z += t.z;
        return *this;
    }
    point3d& operator-=(const point3d &t) {
        x -= t.x;
        y -= t.y;
        z -= t.z;
        return *this;
    }
    point3d& operator*=(ftype t) {
        x *= t;
        y *= t;
        z *= t;
        return *this;
    }
    point3d& operator/=(ftype t) {
        x /= t;
        y /= t;
        z /= t;
        return *this;
    }
    point3d operator+(const point3d &t) const {
        return point3d(*this) += t;
    }
    point3d operator-(const point3d &t) const {
        return point3d(*this) -= t;
    }
    point3d operator*(ftype t) const {
        return point3d(*this) *= t;
    }
    point3d operator/(ftype t) const {
        return point3d(*this) /= t;
    }
};
point3d operator*(ftype a, point3d b) {
    return b * a;
}

در اینجا ftype نوعی داده برای ذخیره‌ی مختصات است که معمولاً int، double یا long long می‌باشد.

ضرب داخلی

تعریف

ضرب داخلی (یا اسکالر) $\mathbf a \cdot \mathbf b$ برای بردارهای $\mathbf a$ و $\mathbf b$ را می‌توان به دو روش معادل تعریف کرد. از نظر هندسی، این ضرب برابر است با حاصل‌ضرب طول بردار اول در طول تصویر بردار دوم بر روی بردار اول. همانطور که در تصویر زیر می‌بینید، این تصویر چیزی جز $|\mathbf b| \cos \theta$ نیست که در آن $\theta$ زاویه‌ی بین $\mathbf a$ و $\mathbf b$ است. بنابراین $\mathbf a\cdot \mathbf b = |\mathbf a| |\mathbf b| \cos \theta$.

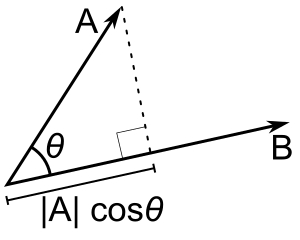
ضرب داخلی دارای چند خاصیت قابل توجه است:

  1. $\mathbf a \cdot \mathbf b = \mathbf b \cdot \mathbf a$
  2. $(\alpha \cdot \mathbf a)\cdot \mathbf b = \alpha \cdot (\mathbf a \cdot \mathbf b)$
  3. $(\mathbf a + \mathbf b)\cdot \mathbf c = \mathbf a \cdot \mathbf c + \mathbf b \cdot \mathbf c$

یعنی، این یک تابع جابه‌جایی‌پذیر است که نسبت به هر دو آرگومان خود خطی است. بردارهای یکه را به صورت زیر نمایش می‌دهیم:

$$\mathbf e_x = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \mathbf e_y = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \mathbf e_z = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}.$$

با این نمادگذاری، می‌توانیم بردار $\mathbf r = (x;y;z)$ را به صورت $r = x \cdot \mathbf e_x + y \cdot \mathbf e_y + z \cdot \mathbf e_z$ بنویسیم. و از آنجایی که برای بردارهای یکه داریم:

$$\mathbf e_x\cdot \mathbf e_x = \mathbf e_y\cdot \mathbf e_y = \mathbf e_z\cdot \mathbf e_z = 1,\\ \mathbf e_x\cdot \mathbf e_y = \mathbf e_y\cdot \mathbf e_z = \mathbf e_z\cdot \mathbf e_x = 0$$

می‌توانیم ببینیم که بر حسب مختصات برای بردارهای $\mathbf a = (x_1;y_1;z_1)$ و $\mathbf b = (x_2;y_2;z_2)$ رابطه‌ی زیر برقرار است:

$$\mathbf a\cdot \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot\mathbf e_y + z_1 \cdot\mathbf e_z)\cdot( x_2 \cdot\mathbf e_x + y_2 \cdot\mathbf e_y + z_2 \cdot\mathbf e_z) = x_1 x_2 + y_1 y_2 + z_1 z_2$$

این تعریف جبری ضرب داخلی نیز هست. از روی این تعریف می‌توانیم توابعی برای محاسبه‌ی آن بنویسیم.

ftype dot(point2d a, point2d b) {
    return a.x * b.x + a.y * b.y;
}
ftype dot(point3d a, point3d b) {
    return a.x * b.x + a.y * b.y + a.z * b.z;
}

هنگام حل مسائل، باید از تعریف جبری برای محاسبه‌ی ضرب داخلی استفاده کرد، اما تعریف هندسی و خواص آن را برای کاربردهایش به خاطر سپرد.

خواص

می‌توانیم بسیاری از خواص هندسی را از طریق ضرب داخلی تعریف کنیم. برای مثال:

  1. نُرم $\mathbf a$ (طول به توان دو): $|\mathbf a|^2 = \mathbf a\cdot \mathbf a$
  2. طول $\mathbf a$: $|\mathbf a| = \sqrt{\mathbf a\cdot \mathbf a}$
  3. تصویر $\mathbf a$ بر روی $\mathbf b$: $\dfrac{\mathbf a\cdot\mathbf b}{|\mathbf b|}$
  4. زاویه‌ی بین بردارها: $\arccos \left(\dfrac{\mathbf a\cdot \mathbf b}{|\mathbf a| \cdot |\mathbf b|}\right)$
  5. از نکته‌ی قبل می‌توان نتیجه گرفت که اگر زاویه‌ی بین دو بردار حاده (تند) باشد، ضرب داخلی مثبت است، اگر منفرجه (باز) باشد، منفی است و اگر بر هم عمود باشند (یعنی زاویه‌ی قائمه بسازند)، برابر با صفر است.

توجه داشته باشید که تمام این توابع به تعداد ابعاد بستگی ندارند، بنابراین برای حالت دو بعدی و سه بعدی یکسان خواهند بود:

ftype norm(point2d a) {
    return dot(a, a);
}
double abs(point2d a) {
    return sqrt(norm(a));
}
double proj(point2d a, point2d b) {
    return dot(a, b) / abs(b);
}
double angle(point2d a, point2d b) {
    return acos(dot(a, b) / abs(a) / abs(b));
}

برای دیدن خاصیت مهم بعدی، به مجموعه‌ی نقاط $\mathbf r$ نگاه می‌کنیم که برای آن‌ها $\mathbf r\cdot \mathbf a = C$ به ازای یک ثابت $C$ برقرار است. می‌توان دید که این مجموعه‌ی نقاط، دقیقاً همان مجموعه‌ی نقاطی است که تصویرشان بر روی $\mathbf a$ برابر با $C \cdot \dfrac{\mathbf a}{|\mathbf a|}$ است و یک اَبَرصفحه‌ی عمود بر $\mathbf a$ تشکیل می‌دهند. در تصویر زیر می‌توانید بردار $\mathbf a$ را به همراه چندین بردار دیگر که با آن ضرب داخلی یکسانی دارند، در فضای دو بعدی مشاهده کنید:

بردارهایی با ضرب داخلی یکسان با a

در فضای دو بعدی، این بردارها یک خط و در فضای سه بعدی، یک صفحه تشکیل می‌دهند. توجه داشته باشید که این نتیجه به ما اجازه می‌دهد یک خط را در فضای دو بعدی به صورت $\mathbf r\cdot \mathbf n=C$ یا $(\mathbf r - \mathbf r_0)\cdot \mathbf n=0$ تعریف کنیم، که در آن $\mathbf n$ بردار عمود بر خط، $\mathbf r_0$ یک بردار دلخواه روی خط و $C = \mathbf r_0\cdot \mathbf n$ است. به همین ترتیب، یک صفحه در فضای سه بعدی قابل تعریف است.

ضرب خارجی

تعریف

فرض کنید سه بردار $\mathbf a$، $\mathbf b$ و $\mathbf c$ در فضای سه بعدی دارید که مطابق تصویر زیر یک متوازی‌السطوح تشکیل می‌دهند:

سه بردار

حجم آن را چگونه محاسبه می‌کنید؟ از دوران مدرسه می‌دانیم که باید مساحت قاعده را در ارتفاع ضرب کنیم، که ارتفاع همان تصویر بردار $\mathbf a$ بر روی جهت عمود بر قاعده است. این بدان معناست که اگر $\mathbf b \times \mathbf c$ را به عنوان برداری تعریف کنیم که هم بر $\mathbf b$ و هم بر $\mathbf c$ عمود است و طول آن برابر با مساحت متوازی‌الاضلاع حاصل از $\mathbf b$ و $\mathbf c$ است، آنگاه $|\mathbf a\cdot (\mathbf b\times\mathbf c)|$ برابر با حجم متوازی‌السطوح خواهد بود. برای حفظ یکپارچگی، می‌گوییم که جهت $\mathbf b\times \mathbf c$ همیشه به گونه‌ای است که چرخش از بردار $\mathbf b$ به سمت بردار $\mathbf c$ از دید ناظری در نوک بردار $\mathbf b\times \mathbf c$ همیشه پادساعتگرد است (تصویر زیر را ببینید).

ضرب خارجی

این تعریف، ضرب خارجی (یا برداری) $\mathbf b\times \mathbf c$ از بردارهای $\mathbf b$ و $\mathbf c$ و حاصل‌ضرب سه‌گانه $\mathbf a\cdot(\mathbf b\times \mathbf c)$ از بردارهای $\mathbf a$، $\mathbf b$ و $\mathbf c$ را مشخص می‌کند.

برخی از خواص قابل توجه ضرب خارجی و ضرب سه‌گانه:

  1. $\mathbf a\times \mathbf b = -\mathbf b\times \mathbf a$
  2. $(\alpha \cdot \mathbf a)\times \mathbf b = \alpha \cdot (\mathbf a\times \mathbf b)$
  3. برای هر $\mathbf b$ و $\mathbf c$، دقیقاً یک بردار $\mathbf r$ وجود دارد به طوری که برای هر بردار $\mathbf a$ داشته باشیم $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf a\cdot\mathbf r$.
    در واقع، اگر دو بردار $\mathbf r_1$ و $\mathbf r_2$ با این خاصیت وجود داشته باشند، آنگاه برای تمام بردارهای $\mathbf a$ داریم $\mathbf a\cdot (\mathbf r_1 - \mathbf r_2)=0$ که این تنها زمانی ممکن است که $\mathbf r_1 = \mathbf r_2$ باشد.
  4. $\mathbf a\cdot (\mathbf b\times \mathbf c) = \mathbf b\cdot (\mathbf c\times \mathbf a) = -\mathbf a\cdot( \mathbf c\times \mathbf b)$

  5. $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$. در واقع برای تمام بردارهای $\mathbf r$، زنجیره معادلات زیر برقرار است:

    $$\mathbf r\cdot( (\mathbf a + \mathbf b)\times \mathbf c) = (\mathbf a + \mathbf b) \cdot (\mathbf c\times \mathbf r) = \mathbf a \cdot(\mathbf c\times \mathbf r) + \mathbf b\cdot(\mathbf c\times \mathbf r) = \mathbf r\cdot (\mathbf a\times \mathbf c) + \mathbf r\cdot(\mathbf b\times \mathbf c) = \mathbf r\cdot(\mathbf a\times \mathbf c + \mathbf b\times \mathbf c)$$

    که با توجه به نکته‌ی ۳، تساوی $(\mathbf a + \mathbf b)\times \mathbf c = \mathbf a\times \mathbf c + \mathbf b\times \mathbf c$ را اثبات می‌کند.

  6. $|\mathbf a\times \mathbf b|=|\mathbf a| \cdot |\mathbf b| \sin \theta$ که در آن $\theta$ زاویه‌ی بین $\mathbf a$ و $\mathbf b$ است، زیرا $|\mathbf a\times \mathbf b|$ برابر با مساحت متوازی‌الاضلاع حاصل از $\mathbf a$ و $\mathbf b$ است.

با توجه به تمام این موارد و این که معادلات زیر برای بردارهای یکه برقرار است:

$$\mathbf e_x\times \mathbf e_x = \mathbf e_y\times \mathbf e_y = \mathbf e_z\times \mathbf e_z = \mathbf 0,\\ \mathbf e_x\times \mathbf e_y = \mathbf e_z,~\mathbf e_y\times \mathbf e_z = \mathbf e_x,~\mathbf e_z\times \mathbf e_x = \mathbf e_y$$

می‌توانیم ضرب خارجی بردارهای $\mathbf a = (x_1;y_1;z_1)$ و $\mathbf b = (x_2;y_2;z_2)$ را به صورت مختصاتی محاسبه کنیم:

$$\mathbf a\times \mathbf b = (x_1 \cdot \mathbf e_x + y_1 \cdot \mathbf e_y + z_1 \cdot \mathbf e_z)\times (x_2 \cdot \mathbf e_x + y_2 \cdot \mathbf e_y + z_2 \cdot \mathbf e_z) =$$
$$(y_1 z_2 - z_1 y_2)\mathbf e_x + (z_1 x_2 - x_1 z_2)\mathbf e_y + (x_1 y_2 - y_1 x_2)\mathbf e_z$$

که می‌توان آن را به شکل زیباتری نیز نوشت:

$$\mathbf a\times \mathbf b = \begin{vmatrix}\mathbf e_x & \mathbf e_y & \mathbf e_z \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix},~a\cdot(b\times c) = \begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{vmatrix}$$

در اینجا $| \cdot |$ نشان‌دهنده‌ی دترمینان یک ماتریس است.

نوعی ضرب خارجی (یعنی حاصل‌ضرب شبه-اسکالر) را می‌توان در حالت دو بعدی نیز پیاده‌سازی کرد. اگر بخواهیم مساحت متوازی‌الاضلاع حاصل از بردارهای $\mathbf a$ و $\mathbf b$ را محاسبه کنیم، باید $|\mathbf e_z\cdot(\mathbf a\times \mathbf b)| = |x_1 y_2 - y_1 x_2|$ را حساب کنیم. راه دیگر برای رسیدن به همین نتیجه، ضرب $|\mathbf a|$ (قاعده متوازی‌الاضلاع) در ارتفاع است، که ارتفاع برابر با تصویر بردار $\mathbf b$ بر روی بردار $\mathbf a$ است که $90$ درجه چرخیده باشد، یعنی $\widehat{\mathbf a}=(-y_1;x_1)$. به عبارت دیگر، محاسبه‌ی $|\widehat{\mathbf a}\cdot\mathbf b|=|x_1y_2 - y_1 x_2|$.

اگر علامت را در نظر بگیریم، در صورتی که چرخش از $\mathbf a$ به $\mathbf b$ (یعنی از دید ناظری در نوک بردار $\mathbf e_z$) پادساعتگرد باشد، مساحت مثبت و در غیر این صورت منفی خواهد بود. این، حاصل‌ضرب شبه-اسکالر را تعریف می‌کند. توجه داشته باشید که این حاصل‌ضرب برابر با $|\mathbf a| \cdot |\mathbf b| \sin \theta$ نیز هست که در آن $\theta$ زاویه‌ی جهت‌دار از $\mathbf a$ به $\mathbf b$ است (اگر چرخش پادساعتگرد باشد مثبت و اگر ساعتگرد باشد منفی است).

بیایید تمام این موارد را پیاده‌سازی کنیم!

point3d cross(point3d a, point3d b) {
    return point3d(a.y * b.z - a.z * b.y,
                   a.z * b.x - a.x * b.z,
                   a.x * b.y - a.y * b.x);
}
ftype triple(point3d a, point3d b, point3d c) {
    return dot(a, cross(b, c));
}
ftype cross(point2d a, point2d b) {
    return a.x * b.y - a.y * b.x;
}

خواص

ضرب خارجی دو بردار $\mathbf a$ و $\mathbf b$ برابر با بردار صفر است اگر و تنها اگر این دو بردار هم‌خط (collinear) باشند (یعنی روی یک خط مشترک قرار بگیرند یا به عبارت دیگر موازی باشند). همین موضوع برای ضرب سه‌گانه نیز صادق است؛ این حاصل‌ضرب برابر با صفر است اگر و تنها اگر بردارهای $\mathbf a$، $\mathbf b$ و $\mathbf c$ هم‌صفحه (coplanar) باشند (یعنی در یک صفحه‌ی مشترک قرار بگیرند).

از این موضوع می‌توانیم معادلات کلی برای تعریف خطوط و صفحات به دست آوریم. یک خط را می‌توان با بردار جهت $\mathbf d$ و یک نقطه‌ی اولیه $\mathbf r_0$ یا با دو نقطه‌ی $\mathbf a$ و $\mathbf b$ تعریف کرد. معادله‌ی آن به صورت $(\mathbf r - \mathbf r_0)\times\mathbf d=0$ یا $(\mathbf r - \mathbf a)\times (\mathbf b - \mathbf a) = 0$ است. برای صفحات، می‌توان آن را با سه نقطه‌ی $\mathbf a$، $\mathbf b$ و $\mathbf c$ به صورت $(\mathbf r - \mathbf a)\cdot((\mathbf b - \mathbf a)\times (\mathbf c - \mathbf a))=0$ یا با یک نقطه‌ی اولیه $\mathbf r_0$ و دو بردار جهت $\mathbf d_1$ و $\mathbf d_2$ که در آن صفحه قرار دارند، به صورت $(\mathbf r - \mathbf r_0)\cdot(\mathbf d_1\times \mathbf d_2)=0$ تعریف کرد.

در فضای دو بعدی، از حاصل‌ضرب شبه-اسکالر می‌توان برای بررسی جهت‌گیری بین دو بردار نیز استفاده کرد، زیرا اگر چرخش از بردار اول به دوم پادساعتگرد باشد، حاصل مثبت و در غیر این صورت منفی است. و البته، می‌توان از آن برای محاسبه‌ی مساحت چندضلعی‌ها استفاده کرد که در مقاله‌ای دیگر توضیح داده شده است. ضرب سه‌گانه را می‌توان برای همین منظور در فضای سه بعدی به کار برد.

تمرین‌ها

تقاطع خطوط

روش‌های ممکن بسیاری برای تعریف یک خط در فضای دو بعدی وجود دارد و نباید در ترکیب آن‌ها تردید کنید. به عنوان مثال، فرض کنید دو خط داریم و می‌خواهیم نقطه‌ی تقاطع آن‌ها را پیدا کنیم. می‌توان گفت تمام نقاط خط اول را می‌توان به صورت $\mathbf r = \mathbf a_1 + t \cdot \mathbf d_1$ پارامتری کرد که در آن $\mathbf a_1$ نقطه‌ی اولیه، $\mathbf d_1$ بردار جهت و $t$ یک پارامتر حقیقی است. برای خط دوم، تمام نقاط آن باید در معادله‌ی $(\mathbf r - \mathbf a_2)\times \mathbf d_2=0$ صدق کنند. از این طریق می‌توانیم به راحتی پارامتر $t$ را پیدا کنیم:

$$(\mathbf a_1 + t \cdot \mathbf d_1 - \mathbf a_2)\times \mathbf d_2=0 \quad\Rightarrow\quad t = \dfrac{(\mathbf a_2 - \mathbf a_1)\times\mathbf d_2}{\mathbf d_1\times \mathbf d_2}$$

بیایید تابعی برای پیدا کردن تقاطع دو خط پیاده‌سازی کنیم.

point2d intersect(point2d a1, point2d d1, point2d a2, point2d d2) {
    return a1 + cross(a2 - a1, d2) / cross(d1, d2) * d1;
}

تقاطع صفحات

با این حال، گاهی اوقات استفاده از بینش‌های هندسی ممکن است دشوار باشد. به عنوان مثال، فرض کنید سه صفحه با نقاط اولیه $\mathbf a_i$ و بردارهای نرمال $\mathbf n_i$ داده شده‌اند و می‌خواهید نقطه‌ی تقاطع آن‌ها را بیابید. ممکن است متوجه شوید که فقط باید دستگاه معادلات زیر را حل کنید:

$$\begin{cases}\mathbf r\cdot \mathbf n_1 = \mathbf a_1\cdot \mathbf n_1, \\ \mathbf r\cdot \mathbf n_2 = \mathbf a_2\cdot \mathbf n_2, \\ \mathbf r\cdot \mathbf n_3 = \mathbf a_3\cdot \mathbf n_3\end{cases}$$

به جای فکر کردن به یک رویکرد هندسی، می‌توانید یک رویکرد جبری را به کار ببرید که بلافاصله به دست می‌آید. به عنوان مثال، با فرض این که از قبل یک کلاس برای نقطه پیاده‌سازی کرده‌اید، حل این دستگاه با استفاده از قاعده‌ی کرامر برای شما آسان خواهد بود، زیرا ضرب سه‌گانه به سادگی همان دترمینان ماتریسی است که از قرار دادن بردارها به عنوان ستون‌های آن به دست می‌آید:

point3d intersect(point3d a1, point3d n1, point3d a2, point3d n2, point3d a3, point3d n3) {
    point3d x(n1.x, n2.x, n3.x);
    point3d y(n1.y, n2.y, n3.y);
    point3d z(n1.z, n2.z, n3.z); 
    point3d d(dot(a1, n1), dot(a2, n2), dot(a3, n3));
    return point3d(triple(d, y, z),
                   triple(x, d, z),
                   triple(x, y, d)) / triple(n1, n2, n3);
}

اکنون می‌توانید خودتان برای آشنا شدن با این مفاهیم، رویکردهایی برای عملیات هندسی رایج پیدا کنید.