مجموعههای مجزا (Disjoint Set Union)¶
این مقاله به بررسی ساختمان داده مجموعههای مجزا یا DSU میپردازد. اغلب به دلیل دو عملیات اصلیاش، Union Find (ادغام-یافتن) نیز نامیده میشود.
این ساختمان داده قابلیتهای زیر را فراهم میکند. به ما چندین عنصر داده شده است که هر کدام یک مجموعه مجزا هستند. یک DSU عملیاتی برای ترکیب هر دو مجموعه خواهد داشت و قادر خواهد بود بگوید که یک عنصر خاص در کدام مجموعه قرار دارد. نسخه کلاسیک آن یک عملیات سوم را نیز معرفی میکند: میتواند از یک عنصر جدید، یک مجموعه بسازد.
بنابراین، رابط کاربری اصلی این ساختمان داده تنها از سه عملیات تشکیل شده است:
make_set(v)- یک مجموعه جدید شامل عنصر جدیدvایجاد میکند.union_sets(a, b)- دو مجموعه مشخص شده را ادغام میکند (مجموعهای که عنصرaدر آن قرار دارد و مجموعهای که عنصرbدر آن قرار دارد).find_set(v)- نماینده (که رهبر نیز نامیده میشود) مجموعهای که عنصرvرا در بر دارد، برمیگرداند. این نماینده، عنصری از مجموعه مربوط به خود است. این نماینده در هر مجموعه توسط خود ساختمان داده انتخاب میشود (و میتواند در طول زمان، به ویژه پس از فراخوانیهایunion_setsتغییر کند). از این نماینده میتوان برای بررسی اینکه آیا دو عنصر در یک مجموعه قرار دارند یا خیر استفاده کرد.aوbدقیقاً در یک مجموعه هستند اگرfind_set(a) == find_set(b). در غیر این صورت، آنها در مجموعههای متفاوتی قرار دارند.
همانطور که بعداً با جزئیات بیشتری توضیح داده میشود، این ساختمان داده به شما امکان میدهد هر یک از این عملیات را به طور متوسط در زمان تقریباً $O(1)$ انجام دهید.
همچنین در یکی از بخشها، ساختار جایگزینی برای DSU توضیح داده شده است که به پیچیدگی متوسط کندتر $O(\log n)$ دست مییابد، اما میتواند از ساختار DSU معمولی قدرتمندتر باشد.
ساخت یک ساختمان داده کارآمد¶
ما مجموعهها را به شکل درخت ذخیره خواهیم کرد: هر درخت با یک مجموعه متناظر خواهد بود. و ریشه درخت، نماینده/رهبر مجموعه خواهد بود.
در تصویر زیر میتوانید نمایش چنین درختانی را مشاهده کنید.
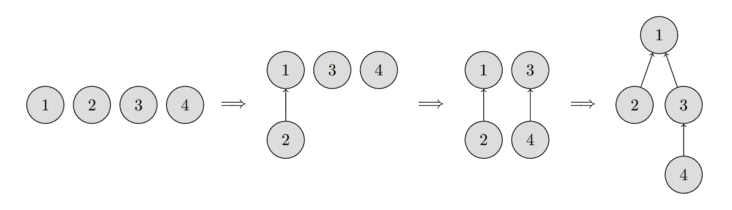
در ابتدا، هر عنصر به عنوان یک مجموعه مجزا شروع میشود، بنابراین هر رأس درخت خودش است. سپس مجموعهای که عنصر ۱ را در بر دارد و مجموعهای که عنصر ۲ را در بر دارد را ترکیب میکنیم. سپس مجموعهای که عنصر ۳ را در بر دارد و مجموعهای که عنصر ۴ را در بر دارد را ترکیب میکنیم. و در مرحله آخر، مجموعهای که عنصر ۱ را در بر دارد و مجموعهای که عنصر ۳ را در بر دارد را ترکیب میکنیم.
برای پیادهسازی، این به این معنی است که ما باید یک آرایه parent را نگهداری کنیم که یک ارجاع به والد بلافصل خود در درخت را ذخیره میکند.
پیادهسازی ساده¶
اکنون میتوانیم اولین پیادهسازی ساختمان داده مجموعههای مجزا را بنویسیم. در ابتدا بسیار ناکارآمد خواهد بود، اما بعداً میتوانیم با استفاده از دو بهینهسازی آن را بهبود بخشیم تا برای هر فراخوانی تابع، تقریباً زمان ثابتی طول بکشد.
همانطور که گفتیم، تمام اطلاعات مربوط به مجموعههای عناصر در یک آرایه parent نگهداری میشود.
برای ایجاد یک مجموعه جدید (عملیات make_set(v)), به سادگی یک درخت با ریشه در رأس v ایجاد میکنیم، به این معنی که v والد خودش است.
برای ترکیب دو مجموعه (عملیات union_sets(a, b)), ابتدا نماینده مجموعهای که a در آن قرار دارد و نماینده مجموعهای که b در آن قرار دارد را پیدا میکنیم.
اگر نمایندهها یکسان باشند، کاری برای انجام دادن نداریم، مجموعهها از قبل ادغام شدهاند.
در غیر این صورت، میتوانیم به سادگی مشخص کنیم که یکی از نمایندهها والد نماینده دیگر است - و به این ترتیب دو درخت را با هم ترکیب میکنیم.
در نهایت پیادهسازی تابع یافتن نماینده (عملیات find_set(v)):
ما به سادگی از والدهای رأس v بالا میرویم تا به ریشه برسیم، یعنی رأسی که ارجاع به والدش به خود آن رأس اشاره دارد.
این عملیات به راحتی به صورت بازگشتی پیادهسازی میشود.
void make_set(int v) {
parent[v] = v;
}
int find_set(int v) {
if (v == parent[v])
return v;
return find_set(parent[v]);
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b)
parent[b] = a;
}
با این حال، این پیادهسازی ناکارآمد است.
ساختن یک مثال که در آن درختان به زنجیرههای طولانی تبدیل شوند، آسان است.
در آن صورت هر فراخوانی find_set(v) میتواند $O(n)$ زمان ببرد.
این از پیچیدگیای که میخواهیم داشته باشیم (نزدیک به زمان ثابت) بسیار دور است. بنابراین دو بهینهسازی را در نظر خواهیم گرفت که به ما امکان میدهد کار را به طور قابل توجهی تسریع کنیم.
بهینهسازی فشردهسازی مسیر (Path compression)¶
این بهینهسازی برای سرعت بخشیدن به find_set طراحی شده است.
اگر ما find_set(v) را برای رأسی مانند v فراخوانی کنیم، در واقع نماینده p را برای تمام رئوسی که در مسیر بین v و نماینده واقعی p قرار دارند، پیدا میکنیم.
ترفند این است که با قرار دادن مستقیم والد هر رأس بازدید شده به p، مسیرها را برای همه آن گرهها کوتاهتر کنیم.
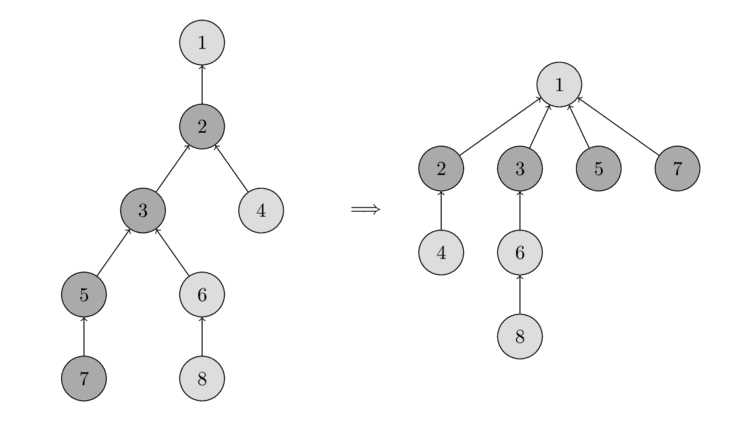
شما میتوانید این عملیات را در تصویر زیر مشاهده کنید.
در سمت چپ یک درخت وجود دارد، و در سمت راست درخت فشردهشده پس از فراخوانی find_set(7) قرار دارد که مسیرها را برای گرههای بازدید شده ۷، ۵، ۳ و ۲ کوتاه میکند.
پیادهسازی جدید find_set به شرح زیر است:
int find_set(int v) {
if (v == parent[v])
return v;
return parent[v] = find_set(parent[v]);
}
این پیادهسازی ساده همان کاری را انجام میدهد که در نظر داشتیم: ابتدا نماینده مجموعه (رأس ریشه) را پیدا میکند و سپس در فرآیند بازگشت از پشته (stack unwinding)، گرههای بازدید شده مستقیماً به نماینده متصل میشوند.
این تغییر ساده در عملیات، به تنهایی به پیچیدگی زمانی $O(\log n)$ به ازای هر فراخوانی به طور متوسط دست مییابد (در اینجا بدون اثبات). یک تغییر دوم وجود دارد که آن را حتی سریعتر میکند.
ادغام بر اساس اندازه / رتبه (Union by size / rank)¶
در این بهینهسازی، ما عملیات union_set را تغییر خواهیم داد.
به طور دقیق، ما تغییر خواهیم داد که کدام درخت به دیگری متصل شود.
در پیادهسازی ساده، درخت دوم همیشه به اولی متصل میشد.
در عمل، این میتواند به درختانی منجر شود که شامل زنجیرههایی به طول $O(n)$ هستند.
با این بهینهسازی، ما با انتخاب دقیق اینکه کدام درخت متصل شود، از این امر جلوگیری خواهیم کرد.
روشهای ممکن زیادی وجود دارد که میتوان از آنها استفاده کرد. محبوبترین آنها دو رویکرد زیر است: در رویکرد اول ما از اندازه درختان به عنوان رتبه استفاده میکنیم، و در رویکرد دوم از عمق درخت استفاده میکنیم (به طور دقیقتر، کران بالای عمق درخت، زیرا با اعمال فشردهسازی مسیر، عمق کاهش مییابد).
در هر دو رویکرد، ماهیت بهینهسازی یکسان است: ما درختی با رتبه پایینتر را به درختی با رتبه بالاتر متصل میکنیم.
در اینجا پیادهسازی ادغام بر اساس اندازه آمده است:
void make_set(int v) {
parent[v] = v;
size[v] = 1;
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (size[a] < size[b])
swap(a, b);
parent[b] = a;
size[a] += size[b];
}
}
و در اینجا پیادهسازی ادغام بر اساس رتبه بر مبنای عمق درختان آمده است:
void make_set(int v) {
parent[v] = v;
rank[v] = 0;
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (rank[a] < rank[b])
swap(a, b);
parent[b] = a;
if (rank[a] == rank[b])
rank[a]++;
}
}
پیچیدگی زمانی¶
همانطور که قبلاً ذکر شد، اگر هر دو بهینهسازی - فشردهسازی مسیر با ادغام بر اساس اندازه / رتبه - را ترکیب کنیم، به پرسوجوهایی با زمان تقریباً ثابت خواهیم رسید. معلوم میشود که پیچیدگی زمانی سرشکن شده نهایی $O(\alpha(n))$ است، که در آن $\alpha(n)$ معکوس تابع آکرمن است که بسیار آهسته رشد میکند. در واقع آنقدر آهسته رشد میکند که برای تمام مقادیر منطقی $n$ (تقریباً $n < 10^{600}$) از $4$ تجاوز نمیکند.
پیچیدگی سرشکن شده، زمان کل به ازای هر عملیات است که در یک دنباله از چندین عملیات ارزیابی میشود. ایده این است که زمان کل کل دنباله را تضمین کنیم، در حالی که اجازه میدهیم عملیاتهای منفرد بسیار کندتر از زمان سرشکن شده باشند. به عنوان مثال، در مورد ما، یک فراخوانی ممکن است در بدترین حالت $O(\log n)$ طول بکشد، اما اگر $m$ فراخوانی از این دست را پشت سر هم انجام دهیم، به طور متوسط به زمان $O(\alpha(n))$ خواهیم رسید.
ما همچنین اثباتی برای این پیچیدگی زمانی ارائه نخواهیم کرد، زیرا بسیار طولانی و پیچیده است.
همچنین، شایان ذکر است که DSU با ادغام بر اساس اندازه / رتبه، اما بدون فشردهسازی مسیر، در زمان $O(\log n)$ به ازای هر پرسوجو کار میکند.
اتصال بر اساس اندیس / اتصال با شیر یا خط (Linking by index / coin-flip linking)¶
هم ادغام بر اساس رتبه و هم ادغام بر اساس اندازه، نیازمند ذخیره دادههای اضافی برای هر مجموعه و نگهداری این مقادیر در هر عملیات ادغام هستند. یک الگوریتم تصادفی نیز وجود دارد که عملیات ادغام را کمی سادهتر میکند: اتصال بر اساس اندیس.
ما به هر مجموعه یک مقدار تصادفی به نام اندیس اختصاص میدهیم و مجموعهای با اندیس کوچکتر را به مجموعهای با اندیس بزرگتر متصل میکنیم. احتمال دارد که یک مجموعه بزرگتر، اندیس بزرگتری نسبت به مجموعه کوچکتر داشته باشد، بنابراین این عملیات به ادغام بر اساس اندازه بسیار نزدیک است. در واقع میتوان ثابت کرد که این عملیات دارای پیچیدگی زمانی مشابهی با ادغام بر اساس اندازه است. با این حال، در عمل کمی کندتر از ادغام بر اساس اندازه است.
شما میتوانید اثبات پیچیدگی و حتی تکنیکهای ادغام بیشتری را اینجا بیابید.
void make_set(int v) {
parent[v] = v;
index[v] = rand();
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (index[a] < index[b])
swap(a, b);
parent[b] = a;
}
}
این یک تصور غلط رایج است که فقط انداختن یک سکه برای تصمیمگیری در مورد اینکه کدام مجموعه را به دیگری متصل کنیم، پیچیدگی یکسانی دارد. با این حال، این درست نیست. مقالهای که در بالا به آن لینک داده شد، حدس میزند که اتصال با شیر یا خط همراه با فشردهسازی مسیر دارای پیچیدگی $\Omega\left(n \frac{\log n}{\log \log n}\right)$ است. و در بنچمارکها، عملکرد آن بسیار بدتر از ادغام بر اساس اندازه/رتبه یا اتصال بر اساس اندیس است.
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (rand() % 2)
swap(a, b);
parent[b] = a;
}
}
کاربردها و بهبودهای مختلف¶
در این بخش، چندین کاربرد از این ساختمان داده، هم استفادههای بدیهی و هم برخی بهبودها در ساختمان داده را بررسی میکنیم.
مؤلفههای همبندی در یک گراف¶
این یکی از کاربردهای واضح DSU است.
به طور رسمی، مسئله به شرح زیر تعریف میشود: در ابتدا ما یک گراف خالی داریم. باید رأسها و یالهای غیرجهتدار را اضافه کنیم و به پرسوجوهایی به شکل $(a, b)$ - "آیا رأسهای $a$ و $b$ در یک مؤلفه همبندی از گراف قرار دارند؟" پاسخ دهیم.
در اینجا میتوانیم مستقیماً از ساختمان داده استفاده کنیم و به راهحلی دست یابیم که اضافه کردن یک رأس یا یال و یک پرسوجو را به طور متوسط در زمان تقریباً ثابت انجام میدهد.
این کاربرد بسیار مهم است، زیرا تقریباً همین مسئله در الگوریتم کراسکال برای یافتن درخت پوشای کمینه ظاهر میشود. با استفاده از DSU میتوانیم پیچیدگی $O(m \log n + n^2)$ را به $O(m \log n)$ بهبود بخشیم.
جستجو برای مؤلفههای همبندی در یک تصویر¶
یکی از کاربردهای DSU وظیفه زیر است: یک تصویر با $n \times m$ پیکسل وجود دارد. در ابتدا همه پیکسلها سفید هستند، اما سپس چند پیکسل سیاه کشیده میشود. شما میخواهید اندازه هر مؤلفه همبندی سفید در تصویر نهایی را تعیین کنید.
برای حل، ما به سادگی روی تمام پیکسلهای سفید تصویر پیمایش میکنیم، برای هر سلول چهار همسایه آن را بررسی میکنیم، و اگر همسایه سفید بود، union_sets را فراخوانی میکنیم.
بنابراین ما یک DSU با $n m$ گره متناظر با پیکسلهای تصویر خواهیم داشت.
درختان حاصل در DSU همان مؤلفههای همبندی مورد نظر هستند.
این مسئله را میتوان با DFS یا BFS نیز حل کرد، اما روش توصیف شده در اینجا یک مزیت دارد: میتواند ماتریس را ردیف به ردیف پردازش کند (یعنی برای پردازش یک ردیف فقط به ردیف قبلی و ردیف فعلی نیاز داریم، و فقط به یک DSU که برای عناصر یک ردیف ساخته شده است نیاز داریم) با حافظه $O(\min(n, m))$.
ذخیره اطلاعات اضافی برای هر مجموعه¶
DSU به شما امکان میدهد به راحتی اطلاعات اضافی را در مجموعهها ذخیره کنید.
یک مثال ساده، اندازه مجموعهها است: ذخیره اندازه در بخش ادغام بر اساس اندازه قبلاً توضیح داده شد (اطلاعات توسط نماینده فعلی مجموعه ذخیره میشد).
به همین ترتیب - با ذخیره آن در گرههای نماینده - میتوانید هر اطلاعات دیگری را در مورد مجموعهها ذخیره کنید.
فشردهسازی پرشها در طول یک قطعه / رنگآمیزی زیرآرایهها به صورت آفلاین¶
یکی از کاربردهای رایج DSU به شرح زیر است: مجموعهای از رأسها وجود دارد و هر رأس یک یال خروجی به رأس دیگری دارد. با DSU میتوانید نقطه پایانی را که پس از دنبال کردن تمام یالها از یک نقطه شروع معین به آن میرسیم، در زمان تقریباً ثابت پیدا کنید.
یک مثال خوب از این کاربرد، مسئله رنگآمیزی زیرآرایهها است. ما یک قطعه به طول $L$ داریم، هر عنصر در ابتدا رنگ ۰ دارد. باید زیرآرایه $[l, r]$ را با رنگ $c$ برای هر پرسوجو $(l, r, c)$ دوباره رنگآمیزی کنیم. در پایان میخواهیم رنگ نهایی هر سلول را پیدا کنیم. فرض میکنیم که همه پرسوجوها را از قبل میدانیم، یعنی وظیفه به صورت آفلاین است.
برای حل، میتوانیم یک DSU بسازیم که برای هر سلول، یک لینک به سلول رنگنشده بعدی را ذخیره کند. بنابراین در ابتدا هر سلول به خودش اشاره میکند. پس از رنگآمیزی یک درخواست رنگآمیزی مجدد یک قطعه، تمام سلولهای آن قطعه به سلول بعد از آن قطعه اشاره خواهند کرد.
حال برای حل این مسئله، پرسوجوها را به ترتیب معکوس در نظر میگیریم: از آخر به اول. به این ترتیب وقتی یک پرسوجو را اجرا میکنیم، فقط باید دقیقاً سلولهای رنگنشده در زیرآرایه $[l, r]$ را رنگ کنیم. همه سلولهای دیگر از قبل رنگ نهایی خود را دارند. برای پیمایش سریع روی تمام سلولهای رنگنشده، از DSU استفاده میکنیم. ما چپترین سلول رنگنشده درون یک قطعه را پیدا میکنیم، آن را دوباره رنگ میکنیم و با اشارهگر به سلول خالی بعدی در سمت راست حرکت میکنیم.
در اینجا میتوانیم از DSU با فشردهسازی مسیر استفاده کنیم، اما نمیتوانیم از ادغام بر اساس رتبه / اندازه استفاده کنیم (زیرا مهم است که چه کسی پس از ادغام، رهبر میشود). بنابراین پیچیدگی به ازای هر ادغام $O(\log n)$ خواهد بود (که آن هم بسیار سریع است).
پیادهسازی:
for (int i = 0; i <= L; i++) {
make_set(i);
}
for (int i = m-1; i >= 0; i--) {
int l = query[i].l;
int r = query[i].r;
int c = query[i].c;
for (int v = find_set(l); v <= r; v = find_set(v)) {
answer[v] = c;
parent[v] = v + 1;
}
}
یک بهینهسازی وجود دارد:
میتوانیم از ادغام بر اساس رتبه استفاده کنیم، اگر سلول رنگنشده بعدی را در یک آرایه اضافی end[] ذخیره کنیم.
سپس میتوانیم دو مجموعه را بر اساس روشهای اکتشافی آنها ادغام کنیم و به راهحلی با پیچیدگی $O(\alpha(n))$ برسیم.
پشتیبانی از فاصله تا نماینده¶
گاهی اوقات در کاربردهای خاص DSU، شما نیاز به نگهداری فاصله بین یک رأس و نماینده مجموعهاش دارید (یعنی طول مسیر در درخت از گره فعلی تا ریشه درخت).
اگر از فشردهسازی مسیر استفاده نکنیم، فاصله فقط تعداد فراخوانیهای بازگشتی است. اما این ناکارآمد خواهد بود.
با این حال، امکان انجام فشردهسازی مسیر وجود دارد، اگر ما فاصله تا والد را به عنوان اطلاعات اضافی برای هر گره ذخیره کنیم.
در پیادهسازی، استفاده از یک آرایه از زوجها برای parent[] راحت است و تابع find_set اکنون دو عدد را برمیگرداند: نماینده مجموعه و فاصله تا آن.
void make_set(int v) {
parent[v] = make_pair(v, 0);
rank[v] = 0;
}
pair<int, int> find_set(int v) {
if (v != parent[v].first) {
int len = parent[v].second;
parent[v] = find_set(parent[v].first);
parent[v].second += len;
}
return parent[v];
}
void union_sets(int a, int b) {
a = find_set(a).first;
b = find_set(b).first;
if (a != b) {
if (rank[a] < rank[b])
swap(a, b);
parent[b] = make_pair(a, 1);
if (rank[a] == rank[b])
rank[a]++;
}
}
پشتیبانی از زوجیت طول مسیر / بررسی دو بخشی بودن به صورت آنلاین¶
همانند محاسبه طول مسیر تا رهبر، میتوان زوجیت طول مسیر تا آن را نیز نگهداری کرد. چرا این کاربرد در یک پاراگراف جداگانه آمده است؟
نیاز غیرمعمول به ذخیره زوجیت مسیر در وظیفه زیر مطرح میشود: در ابتدا به ما یک گراف خالی داده میشود، میتوان به آن یال اضافه کرد، و ما باید به پرسوجوهایی به این شکل پاسخ دهیم: "آیا مؤلفه همبندی حاوی این رأس دو بخشی است؟".
برای حل این مسئله، ما یک DSU برای ذخیره مؤلفهها میسازیم و زوجیت مسیر تا نماینده را برای هر رأس ذخیره میکنیم. بنابراین میتوانیم به سرعت بررسی کنیم که آیا اضافه کردن یک یال منجر به نقض خاصیت دو بخشی بودن میشود یا خیر: یعنی اگر دو سر یال در یک مؤلفه همبندی قرار داشته باشند و طول مسیر با زوجیت یکسان تا رهبر داشته باشند، اضافه کردن این یال یک دور به طول فرد ایجاد میکند و مؤلفه خاصیت دو بخشی بودن را از دست میدهد.
تنها مشکلی که با آن روبرو هستیم، محاسبه زوجیت در متد union_find است.
اگر یال $(a, b)$ را اضافه کنیم که دو مؤلفه همبندی را به هم متصل میکند، آنگاه هنگام اتصال یک درخت به دیگری باید زوجیت را تنظیم کنیم.
بیایید فرمولی را استخراج کنیم که زوجیت اختصاص داده شده به رهبر مجموعهای که به مجموعه دیگر متصل میشود را محاسبه میکند. فرض کنید $x$ زوجیت طول مسیر از رأس $a$ تا رهبرش $A$ باشد، و $y$ زوجیت طول مسیر از رأس $b$ تا رهبرش $B$ باشد، و $t$ زوجیت مورد نظری باشد که باید پس از ادغام به $B$ اختصاص دهیم. مسیر از سه بخش تشکیل شده است: از $B$ به $b$، از $b$ به $a$ که توسط یک یال متصل شده و بنابراین زوجیت $1$ دارد، و از $a$ به $A$. بنابراین فرمول زیر را به دست میآوریم (علامت $\oplus$ نشاندهنده عملیات XOR است):
بنابراین صرف نظر از اینکه چند ادغام انجام میدهیم، زوجیت یالها از یک رهبر به دیگری منتقل میشود.
ما پیادهسازی DSU که از زوجیت پشتیبانی میکند را ارائه میدهیم. همانند بخش قبل، از یک زوج برای ذخیره والد و زوجیت استفاده میکنیم. علاوه بر این، برای هر مجموعه در آرایه bipartite[] ذخیره میکنیم که آیا هنوز دو بخشی است یا خیر.
void make_set(int v) {
parent[v] = make_pair(v, 0);
rank[v] = 0;
bipartite[v] = true;
}
pair<int, int> find_set(int v) {
if (v != parent[v].first) {
int parity = parent[v].second;
parent[v] = find_set(parent[v].first);
parent[v].second ^= parity;
}
return parent[v];
}
void add_edge(int a, int b) {
pair<int, int> pa = find_set(a);
a = pa.first;
int x = pa.second;
pair<int, int> pb = find_set(b);
b = pb.first;
int y = pb.second;
if (a == b) {
if (x == y)
bipartite[a] = false;
} else {
if (rank[a] < rank[b])
swap (a, b);
parent[b] = make_pair(a, x^y^1);
bipartite[a] &= bipartite[b];
if (rank[a] == rank[b])
++rank[a];
}
}
bool is_bipartite(int v) {
return bipartite[find_set(v).first];
}
پرسش کمینه بازه (RMQ) به صورت آفلاین در $O(\alpha(n))$ به طور متوسط / ترفند آرپا¶
به ما یک آرایه a[] داده شده و باید کمینهها را در بازههای مشخصی از آرایه محاسبه کنیم.
ایده حل این مسئله با DSU به شرح زیر است:
ما روی آرایه پیمایش میکنیم و وقتی در عنصر i-ام هستیم، به تمام پرسوجوهای (L, R) با R == i پاسخ خواهیم داد.
برای انجام این کار به طور کارآمد، یک DSU با استفاده از i عنصر اول با ساختار زیر نگهداری میکنیم: والد یک عنصر، عنصر کوچکتر بعدی در سمت راست آن است.
سپس با استفاده از این ساختار، پاسخ به یک پرسوجو a[find_set(L)] خواهد بود، یعنی کوچکترین عدد در سمت راست L.
این رویکرد به وضوح فقط به صورت آفلاین کار میکند، یعنی اگر همه پرسوجوها را از قبل بدانیم.
به راحتی میتوان دید که میتوانیم از فشردهسازی مسیر استفاده کنیم. و همچنین میتوانیم از ادغام بر اساس رتبه استفاده کنیم، اگر رهبر واقعی را در یک آرایه جداگانه ذخیره کنیم.
struct Query {
int L, R, idx;
};
vector<int> answer;
vector<vector<Query>> container;
container[i] شامل تمام پرسوجوهایی است که R == i دارند.
stack<int> s;
for (int i = 0; i < n; i++) {
while (!s.empty() && a[s.top()] > a[i]) {
parent[s.top()] = i;
s.pop();
}
s.push(i);
for (Query q : container[i]) {
answer[q.idx] = a[find_set(q.L)];
}
}
امروزه این الگوریتم به عنوان ترفند آرپا شناخته میشود. این نام از امیررضا پورآخوان گرفته شده است که به طور مستقل این تکنیک را کشف و محبوب کرد. هرچند این الگوریتم قبل از کشف او نیز وجود داشته است.
کوچکترین جد مشترک (LCA) به صورت آفلاین در $O(\alpha(n))$ به طور متوسط¶
الگوریتم یافتن LCA در مقاله کوچکترین جد مشترک - الگوریتم آفلاین تارجان مورد بحث قرار گرفته است. این الگوریتم به دلیل سادگیاش (به ویژه در مقایسه با یک الگوریتم بهینه مانند الگوریتم Farach-Colton و Bender) با سایر الگوریتمهای یافتن LCA مقایسه مطلوبی دارد.
ذخیره DSU به طور صریح در یک لیست مجموعه / کاربردهای این ایده هنگام ادغام ساختمان دادههای مختلف¶
یکی از راههای جایگزین برای ذخیره DSU، حفظ هر مجموعه به شکل یک لیست صریح از عناصر آن است. همزمان، هر عنصر نیز ارجاعی به نماینده مجموعه خود را ذخیره میکند.
در نگاه اول این یک ساختمان داده ناکارآمد به نظر میرسد: با ترکیب دو مجموعه، باید یک لیست را به انتهای لیست دیگر اضافه کنیم و رهبری را در تمام عناصر یکی از لیستها بهروز کنیم.
با این حال، معلوم میشود که استفاده از یک روش اکتشافی وزنی (مشابه ادغام بر اساس اندازه) میتواند به طور قابل توجهی پیچیدگی مجانبی را کاهش دهد: $O(m + n \log n)$ برای انجام $m$ پرسوجو روی $n$ عنصر.
منظور از روش اکتشافی وزنی این است که ما همیشه مجموعه کوچکتر را به مجموعه بزرگتر اضافه خواهیم کرد.
اضافه کردن یک مجموعه به دیگری به راحتی در union_sets قابل پیادهسازی است و زمانی متناسب با اندازه مجموعه اضافه شده خواهد برد.
و جستجوی رهبر در find_set با این روش ذخیرهسازی، $O(1)$ طول خواهد کشید.
بیایید پیچیدگی زمانی $O(m + n \log n)$ را برای اجرای $m$ پرسوجو اثبات کنیم.
ما یک عنصر دلخواه $x$ را ثابت میکنیم و تعداد دفعاتی که در عملیات ادغام union_sets لمس شده است را میشماریم.
هنگامی که عنصر $x$ برای اولین بار لمس میشود، اندازه مجموعه جدید حداقل $2$ خواهد بود.
هنگامی که برای دومین بار لمس میشود، مجموعه حاصل اندازهای حداقل $4$ خواهد داشت، زیرا مجموعه کوچکتر به بزرگتر اضافه میشود.
و به همین ترتیب.
این بدان معناست که $x$ فقط میتواند در حداکثر $\log n$ عملیات ادغام جابجا شود.
بنابراین، مجموع روی تمام رأسها $O(n \log n)$ به علاوه $O(1)$ برای هر درخواست را به ما میدهد.
در اینجا یک پیادهسازی آمده است:
vector<int> lst[MAXN];
int parent[MAXN];
void make_set(int v) {
lst[v] = vector<int>(1, v);
parent[v] = v;
}
int find_set(int v) {
return parent[v];
}
void union_sets(int a, int b) {
a = find_set(a);
b = find_set(b);
if (a != b) {
if (lst[a].size() < lst[b].size())
swap(a, b);
while (!lst[b].empty()) {
int v = lst[b].back();
lst[b].pop_back();
parent[v] = a;
lst[a].push_back (v);
}
}
}
این ایده اضافه کردن بخش کوچکتر به بخش بزرگتر میتواند در بسیاری از راهحلهایی که هیچ ارتباطی با DSU ندارند نیز استفاده شود.
برای مثال، مسئله زیر را در نظر بگیرید: به ما یک درخت داده شده است، هر برگ یک عدد به آن اختصاص داده شده است (یک عدد ممکن است چندین بار در برگهای مختلف ظاهر شود). ما میخواهیم تعداد اعداد مختلف در زیردرخت را برای هر گره درخت محاسبه کنیم.
با اعمال همین ایده به این وظیفه، میتوان به این راهحل دست یافت: میتوانیم یک DFS پیادهسازی کنیم که یک اشارهگر به مجموعهای از اعداد صحیح - لیست اعداد در آن زیردرخت - را برمیگرداند. سپس برای به دست آوردن پاسخ برای گره فعلی (مگر اینکه البته برگ باشد)، DFS را برای همه فرزندان آن گره فراخوانی میکنیم و همه مجموعههای دریافتی را با هم ادغام میکنیم. اندازه مجموعه حاصل، پاسخ برای گره فعلی خواهد بود. برای ترکیب کارآمد چندین مجموعه، ما فقط دستورالعمل توصیف شده در بالا را اعمال میکنیم: ما مجموعهها را با اضافه کردن مجموعههای کوچکتر به بزرگترها ادغام میکنیم. در پایان، به یک راهحل $O(n \log^2 n)$ میرسیم، زیرا یک عدد فقط حداکثر $O(\log n)$ بار به یک مجموعه اضافه خواهد شد.
ذخیره DSU با نگهداری یک ساختار درختی واضح / یافتن پل به صورت آنلاین در $O(\alpha(n))$ به طور متوسط¶
یکی از قدرتمندترین کاربردهای DSU این است که به شما امکان میدهد آن را هم به صورت درختان فشرده و هم غیرفشرده ذخیره کنید. فرم فشرده میتواند برای ادغام درختان و برای تأیید اینکه آیا دو رأس در یک درخت هستند استفاده شود، و فرم غیرفشرده میتواند - برای مثال - برای جستجوی مسیر بین دو رأس داده شده یا سایر پیمایشهای ساختار درخت استفاده شود.
در پیادهسازی، این به این معنی است که علاوه بر آرایه والد فشرده parent[]، ما باید آرایه والد غیرفشرده real_parent[] را نیز نگهداری کنیم.
بدیهی است که نگهداری این آرایه اضافی، پیچیدگی را بدتر نخواهد کرد:
تغییرات در آن فقط زمانی رخ میدهد که دو درخت را ادغام میکنیم، و فقط در یک عنصر.
از سوی دیگر، در کاربردهای عملی، ما اغلب نیاز به اتصال درختان با استفاده از یک یال مشخص داریم، نه با استفاده از دو گره ریشه. این بدان معناست که ما چارهای جز ریشهدار کردن مجدد یکی از درختان نداریم (قرار دادن انتهای یال به عنوان ریشه جدید درخت).
در نگاه اول به نظر میرسد که این ریشهدار کردن مجدد بسیار پرهزینه است و پیچیدگی زمانی را به شدت بدتر میکند.
در واقع، برای ریشهدار کردن یک درخت در رأس $v$، باید از آن رأس به ریشه قدیمی برویم و جهتها را در parent[] و real_parent[] برای همه گرههای آن مسیر تغییر دهیم.
با این حال، در واقعیت آنقدرها هم بد نیست، ما میتوانیم مشابه ایدههای بخشهای قبلی، درخت کوچکتر از دو درخت را ریشهدار کنیم و به طور متوسط به پیچیدگی $O(\log n)$ برسیم.
جزئیات بیشتر (شامل اثبات پیچیدگی زمانی) را میتوان در مقاله یافتن پلها به صورت آنلاین یافت.
نگاهی به تاریخچه¶
ساختمان داده DSU از دیرباز شناخته شده است.
این روش ذخیرهسازی این ساختار به شکل جنگلی از درختان ظاهراً برای اولین بار توسط گالر و فیشر در سال ۱۹۶۴ توصیف شد (Galler, Fisher, "An Improved Equivalence Algorithm)، با این حال تحلیل کامل پیچیدگی زمانی آن بسیار دیرتر انجام شد.
بهینهسازیهای فشردهسازی مسیر و ادغام بر اساس رتبه توسط مکایلروی و موریس و به طور مستقل از آنها توسط تریتر توسعه یافت.
هاپکرافت و اولمن در سال ۱۹۷۳ پیچیدگی زمانی $O(\log^\star n)$ را نشان دادند (Hopcroft, Ullman "Set-merging algorithms") - در اینجا $\log^\star$ لگاریتم مکرر است (این یک تابع با رشد کند است، اما هنوز به کندی معکوس تابع آکرمن نیست).
برای اولین بار، ارزیابی $O(\alpha(n))$ در سال ۱۹۷۵ نشان داده شد (Tarjan "Efficiency of a Good But Not Linear Set Union Algorithm"). بعدها در سال ۱۹۸۵، او به همراه لیوون، تحلیلهای پیچیدگی متعددی را برای چندین روش رتبهبندی مختلف و راههای فشردهسازی مسیر منتشر کرد (Tarjan, Leeuwen "Worst-case Analysis of Set Union Algorithms").
سرانجام در سال ۱۹۸۹، فردمن و ساکس ثابت کردند که در مدل محاسباتی پذیرفته شده، هر الگوریتمی برای مسئله مجموعههای مجزا باید به طور متوسط حداقل در زمان $O(\alpha(n))$ کار کند (Fredman, Saks, "The cell probe complexity of dynamic data structures").